
已知二次函数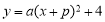 的图象是由函数
的图象是由函数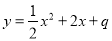 的图象向左平移一个单位得到.反比例函数
的图象向左平移一个单位得到.反比例函数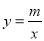 与二次函数
与二次函数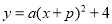 的图象交于点A(1,n).
的图象交于点A(1,n).
(1)求a,p,q,m,n的值;
(2)要使反比例函数和二次函数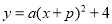 在直线
在直线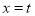 的一侧都是y随着x的增大而减小,求t的最大值;
的一侧都是y随着x的增大而减小,求t的最大值;
(3)记二次函数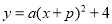 图象的顶点为B,以AB为边构造矩形ABCD,边CD与函数
图象的顶点为B,以AB为边构造矩形ABCD,边CD与函数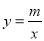 相交,且直线AB与CD的距离为
相交,且直线AB与CD的距离为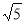 ,求出点D,C的坐标.
,求出点D,C的坐标.
(1)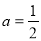 ,p=3,q=6,m=12,n=12;(2)-3;(3)D的坐标为(3,11),点C(﹣1,3).
,p=3,q=6,m=12,n=12;(2)-3;(3)D的坐标为(3,11),点C(﹣1,3).
【解析】
试题分析:(1)先将函数y=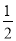 x2+2x+q配方,即可得到顶点坐标(-2,q-2),根据平移的性质可得a=
x2+2x+q配方,即可得到顶点坐标(-2,q-2),根据平移的性质可得a=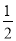 ,p=3,q=6,再把x=1,y=n代入y=
,p=3,q=6,再把x=1,y=n代入y=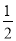 (x+3)2+4,把x=1,y=12代入y=
(x+3)2+4,把x=1,y=12代入y=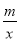 可求m,n的值;
可求m,n的值;
(2)根据反比例函数的增减性,二次函数y=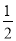 (x+3)2+4的对称轴和增减性,即可求得t的最大值;
(x+3)2+4的对称轴和增减性,即可求得t的最大值;
(3)过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.,根据勾股定理,矩形的性质,相似三角形的判定和性质,即可求得点D,C的坐标.
试题解析:【解析】
(1)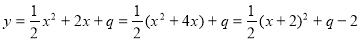 ,顶点坐标(﹣2,q﹣2)
,顶点坐标(﹣2,q﹣2)
(或用顶点坐标公式)
∴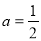 ,p=3,q=6,
,p=3,q=6,
把x=1,y=n代入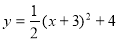 得n=12;
得n=12;
把x=1,y=12代入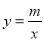 得m=12;
得m=12;
(2)∵反比例函数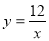 在图象所在的每一象限内,y随着x的增大而减小
在图象所在的每一象限内,y随着x的增大而减小
而二次函数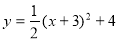 的对称轴为:直线x=﹣3
的对称轴为:直线x=﹣3
要使二次函数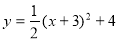 满足上述条件,x≤﹣3
满足上述条件,x≤﹣3
∴t的最大值为﹣3;
(3)如图,过点A作直线l∥x轴,作DF⊥l于F,BE⊥l于E.
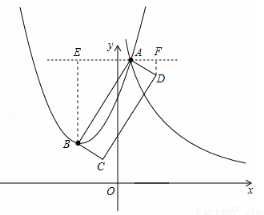
∵点B的坐标为(﹣3,4),A(1,12)
∴AE=4,BE=8
∵BE⊥l,
∴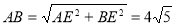
∵四边形ABCD是矩形,
∴∠BAD=90°,∴∠EAB+∠FAD=90°
∵BE⊥l于E,
∴∠EAB+∠EBA=90°∴∠FAD=∠EBA
∴Rt△EBA∽Rt△FAD∴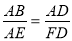
又∵AD=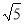 ,
,
∴FD=1
同理:AF=2
∴点D的坐标为(3,11)
同理可求点C(﹣1,3).
考点:二次函数综合题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源:[同步]2015年课时同步练习(人教版)八年级数学下册18.1(解析版) 题型:选择题
(2012湖北武汉)在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.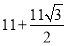
B.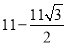
C.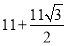 或
或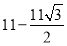
D.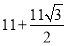 或
或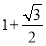
查看答案和解析>>
科目:初中数学 来源: 题型:
如图 ,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )

A.8米 B.10米 C.12米 D.14米
查看答案和解析>>
科目:初中数学 来源:[同步]2015年课时同步练习(人教版)八年级数学下册18.1(解析版) 题型:解答题
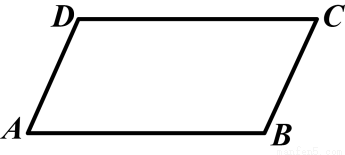
(2013广东)如图,已知□ABCD.
(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图,保留作图痕迹,不要求写作法).
(2)在(1)的条件下,连接AE,交CD于点F,求证:△AFD≌△EFC.
查看答案和解析>>
科目:初中数学 来源:[同步]2015年课时同步练习(人教版)八年级数学下册18.1(解析版) 题型:选择题
(2013哈尔滨)如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )

A.4
B.3
C.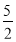
D.2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
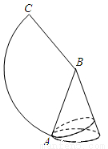
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC= ;S△DEF:S△ADE = 。
查看答案和解析>>
科目:初中数学 来源: 题型:
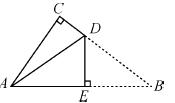
如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:填空题
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com