【题目】已知抛物线
(1)写出该抛物线的顶点D坐标和对称轴.
(2)抛物线与
轴交于A,B两点，求△ABD的面积
【答案】（1）（-1,4），直线
= -1（2）8
【解析】（1）将二次函数配方后即可求得其顶点坐标及对称轴；
（2）根据上题确定的二次函数的顶点坐标和抛物线与坐标轴的交点坐标就能够求得△ABD的面积.
解：（1）由y=-x2-2x+3= -( x2+2x-3)=-( x2+2x+1-3-1)= -（x+1）2+4,
∴该抛物线的顶点D坐标为（-1,4）对称轴x=-1,
（2）令y=0，-x2-2x+3=0，则x2+2x-3=0，
（x+3）（x-1）=0，x1=-3，x2=1，
∴A（-3，0），B（1，0）.
又∵D（-1，4），
∴AB=4，OC=4，
∴S△ABC=
AB×OC=
×4×4=8.
“点睛”本题考查了二次函数的性质，解题的关键是能够利用配方法确定二次函数的顶点坐标和抛物线与坐标轴的交点坐标，难度不大.
科目：初中数学 来源： 题型：
【题目】如图①，将笔记本活页一角折过去，使角的顶点A落在A′处，BC为折痕．
(1)图①中，若∠1=30
，求∠A′BD的艘数；
(2)如果将图①的另一角∠A′BD斜折过去，使BD边与BA′重合，折痕为BE，点D的对应点为D′，如图②所示．∠1=30
，求∠2以及∠CBE的度数；
(3)如果将图①的另一角斜折过去，使BD边落在∠l内部，折痕为BE，点D的对应点为D′，如图③所示，若∠1=40
，设∠A′BD′=α，∠EBD=β，请直接回答：
①α的取值范围和β的取值范围：
②α与β之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线
与
轴、
轴分别相交于点A，B，四边形ABCD是正方形，抛物线
在经过A，D两点.
（1）求该抛物线表达式；
（2）连接BD，将线段BD绕着D点顺时针旋转90度，得到DB’.直接写出点B’的坐标，并判断点B’是否落在抛物线上，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（ ）
①∠AOB=∠COD；
②∠AOB+∠COD=90°；
③∠BOC+∠AOD=180°；
④∠AOC-∠COD=∠BOC．
A．①②③
B．①②④
C．①③④
D．②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=﹣（x﹣1）2+4，
（1）求出二次函数的顶点坐标及与x轴交点坐标，结合开口方向再在网格中画出草图．
（2）观察图象确定：x取何值时，y随着x的增大而增大，当X取何值时，y随着x的增大而减少．
（3）观察图象确定：x取何值时y＞0，x取何值时y＜0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）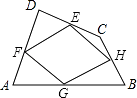 
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
