
【题目】已知![]() 是最大的负整数,
是最大的负整数,![]() 是多项式
是多项式![]() 的次数,
的次数,![]() 是单项式
是单项式![]() 的系数,且
的系数,且![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 在数轴上对应的数.
在数轴上对应的数.
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 出发沿数轴负方向运动,点
出发沿数轴负方向运动,点![]() 的速度是每秒
的速度是每秒![]() 个单位长度,点
个单位长度,点![]() 的速度是每秒2个单位长度,在数轴上-10处竖立一块档板,运动点碰到档板后马上沿反方向返回,当
的速度是每秒2个单位长度,在数轴上-10处竖立一块档板,运动点碰到档板后马上沿反方向返回,当![]() 运动到档板时两点向时停止运动,求当运动几秒后,点
运动到档板时两点向时停止运动,求当运动几秒后,点![]() 碰到点
碰到点![]() ?并求此位置在数轴上表示的数;
?并求此位置在数轴上表示的数;
(3)在数轴上找一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和等于13,请直接写出所有点
三点的距离之和等于13,请直接写出所有点![]() 对应的数.(不必说明理由)
对应的数.(不必说明理由)
![]()
【答案】(1)![]() ,
,![]() ;(2) 当运动9秒后,点Q碰到点P,此位置在数轴上表示的数为0 ;(3) 当点M对应的数为
;(2) 当运动9秒后,点Q碰到点P,此位置在数轴上表示的数为0 ;(3) 当点M对应的数为![]() 或
或![]() 时,点M到A、B、C三点的距离之和等于13
时,点M到A、B、C三点的距离之和等于13
【解析】
(1)根据有理数、多项式和单项式的相关概念,即可求出![]() 、
、![]() 、
、![]() 的值;
的值;
(2)根据数轴上两点间的距离公式求得路程,再路程、速度、时间的关系进行求解;
(3)分点M在点B的右侧、BC之间、AC之间、点A的左侧四种情况讨论,分别列方程可求得答案.
(1)最大的负整数是![]() ,多项式
,多项式![]() 的次数是6,单项式
的次数是6,单项式![]() 的系数是
的系数是![]() ,
,
∴![]() ,
,![]() ;
;
(2)设当运动t秒后,点P与Q相遇,
依题意得:![]() ,
,
解得:![]() ,
,
此时点P的坐标为:![]() ,即原点,
,即原点,
故答数为:当运动9秒后,点Q碰到点P,此位置在数轴上表示的数为0 ;
(3)设点M对应的数为![]() ,使P到A、B、C的距离和等于13,
,使P到A、B、C的距离和等于13,
![]()
①当M在点B的右侧,![]() ,
,
解得:![]() ,因为
,因为![]() ,不符合题意,舍去;
,不符合题意,舍去;
②当M在BC之间,![]() ,
,
解得:![]() ;
;
③当M在AC之间,![]() ,
,
解得:![]() (不符合题意,舍去);
(不符合题意,舍去);
④当M在点A的左侧,![]() ,
,
解得:![]() ;
;
综上,当点M对应的数为![]() 或
或![]() 时,点M到A、B、C三点的距离之和等于13.
时,点M到A、B、C三点的距离之和等于13.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】已知:将矩形纸片ABCD折叠,使点A与点C重合(点D与D'为对应点),折痕为EF,连接AF.
(1)如图1,求证:四边形AECF为菱形;
(2)如图2,若FC=2DF,连接AC交EF于点O,连接DO、D'O,在不添加任何辅助线的情况下,请直接写出图2中所有等边三角形.
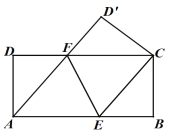

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题;
(1)4(a3)4﹣(3a6)2
(2)﹣6xy(x﹣2y)
(3)(9x2y﹣6xy2)÷3xy
(4)(a+2b)(a﹣2b)﹣(a+b)2
(5)(﹣12)0+2﹣2
(6)20182﹣2017×2019(用公式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图, 在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结
,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结![]() 交边AB于点
交边AB于点![]() .
.
(1)求AD的长;
(2)设![]() ,
,![]() 的面积为y, 求y关于x的函数解析式,并写出定义域;
的面积为y, 求y关于x的函数解析式,并写出定义域;
(3)过点C作![]() , 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,
, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,![]() 为等边三角形?请指出点P的位置并加以证明.
为等边三角形?请指出点P的位置并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
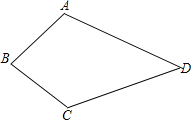
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
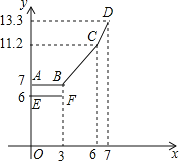
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________;若BN、CN分别平分∠ABC,∠ACB的外角,则∠N=_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com