
����Ŀ��Ϊ�����ͼ����Ǹ������ҵ�����ijɱ�ѹ����ij����2018��11��17���𣬵�������˼ۣ��������������б���ͼ������a��b��cΪ������
��ʻ·�� | �շѱ� | |
����ǰ | ���ۺ� | |
������3km�IJ��� | ��6Ԫ | ��a Ԫ |
����3km������6km�IJ��� | ÿ����2.1Ԫ | ÿ����bԪ |
����6km�IJ��� | ÿ����cԪ | |
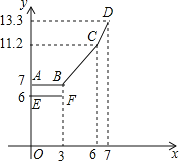
����ʻ·��xkmʱ������ǰ���˼�y1��Ԫ�������ۺ���˼�Ϊy2��Ԫ����ͼ������ABCD��ʾy2��x֮��ĺ�����ϵʽ���߶�EF��ʾ��0��x��3ʱ��y1��x�ĺ�����ϵʽ������ͼ����Ϣ��������и��⣺
��1����գ�a=�� ����b=�� ����c=�� ����
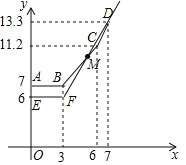
��2��д����x��3ʱ��y1��x�Ĺ�ϵ��������ͼ�л����ú�����ͼ����
��3������y1��y2��ͼ���Ƿ���ڽ��㣿�����ڣ������������꣬��˵���õ��ʵ�����壬����������˵�����ɣ�
���𰸡���1��7��1.4��2.1����2��y1=2.1x��0.3��ͼ�����������3������y1��y2��ͼ����ڽ��㣨![]() ��9����������Ϊ�� x<
��9����������Ϊ�� x<![]() ʱ�Ƿ�������ǰ���㣬��x>
ʱ�Ƿ�������ǰ���㣬��x>![]() ʱ�������ۺ���㣮
ʱ�������ۺ���㣮
����������1��a��ͼ��ֱ�ӵó���b��c���ݣ��˼���·��=���ۣ�������ֵ��������ɣ�
��2����x��3ʱ��y1��x�Ĺ�ϵ������������ɣ���һ����Ϊ��6���ڶ�����Ϊ��x��3����2.1�����ԣ���������ӣ��Ϳɵõ�����ʽ�����ɻ���ͼ����
��3����y1=y2ʱ��������ڣ����x��ֵ���ٴ�������һ��ʽ���У����ܵõ�yֵ��yֵ���������ָ�˼�.
����ͼ��֪��a=7Ԫ��
b=��11.2��7���£�6��3��=1.4Ԫ��
c=��13.3��11.2���£�7��6��=2.1Ԫ��
�ʴ�Ϊ7��1.4��2.1��
����ͼ�ã���x��3ʱ��y1��x�Ĺ�ϵʽ�ǣ�
y1=6+��x��3����2.1��
�����ã�y1=2.1x��0.3��
����ͼ����ͼ��ʾ��
����ͼ�ã���3��x��6ʱ��y2��x�Ĺ�ϵʽ�ǣ�
y2=7+��x��3����1.4��
�����ã�y2=1.4x+2.8��
���ԣ���y1=y2ʱ��������ڣ�
����2.1x��0.3=1.4x+2.8��
��ã�x=![]() ��y=9��
��y=9��
���ԣ�����y1��y2��ͼ����ڽ��㣨![]() ��9����
��9����
������Ϊ�� x<![]() ʱ�Ƿ�������ǰ���㣬�� x>
ʱ�Ƿ�������ǰ���㣬�� x>![]() ʱ�������ۺ���㣮
ʱ�������ۺ���㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ɽ�����¹س��ǡ���ĸ�������������ǽڼ���������ȵ㾰����ij��ѧ�����꼶��1����ѧ��������ٵ�������������ļƻ�����ȫ����飬������ĸ����A������������B��������������C����һ��������D�������������������森���ݵ���Ľ�������˲���ȫ������ͳ��ͼ������ͳ��ͼ����ͼ�١�ͼ�ڣ����£������ͼ����������Ϣ������������⣺
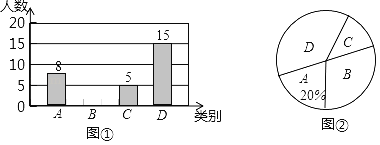
��1�������꼶��1����ѧ��������
��2��������ͳ��ͼ����������
��3��������ͳ��ͼ�б�ʾ��B�������Բ�ĽǵĶ�����
��4��������ѧ���꼶��ѧ��520�ˣ���ƻ����ѡ��A��B��C��������ȥ�����ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �����ĸ�������
�����ĸ�������![]() �Ƕ���ʽ
�Ƕ���ʽ![]() �Ĵ�����
�Ĵ�����![]() �ǵ���ʽ
�ǵ���ʽ![]() ��ϵ������
��ϵ������![]() ��
��![]() ��
��![]() �ֱ��ǵ�
�ֱ��ǵ�![]() ��
��![]() ��
��![]() �������϶�Ӧ������
�������϶�Ӧ������
��1����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2��������![]() ��
��![]() ͬʱ��
ͬʱ��![]() ��
��![]() ���������Ḻ�����˶�����
���������Ḻ�����˶�����![]() ���ٶ���ÿ��
���ٶ���ÿ��![]() ����λ���ȣ���
����λ���ȣ���![]() ���ٶ���ÿ��2����λ���ȣ���������-10������һ�鵵�壬�˶�����������������ط����أ���
���ٶ���ÿ��2����λ���ȣ���������-10������һ�鵵�壬�˶�����������������ط����أ���![]() �˶�������ʱ������ʱֹͣ�˶������˶������
�˶�������ʱ������ʱֹͣ�˶������˶������![]() ������
������![]() �������λ���������ϱ�ʾ������
�������λ���������ϱ�ʾ������
��3������������һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��
��![]() ��
��![]() ����ľ���֮�͵���13����ֱ��д�����е�
����ľ���֮�͵���13����ֱ��д�����е�![]() ��Ӧ������������˵�����ɣ�
��Ӧ������������˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�BC��AB��E��AD��һ�㣬��ABE��BE�۵�����Aǡ�������߶�CE�ϵĵ�F����
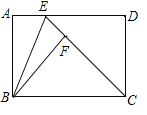
��1����֤��CF��DE��
��2����![]() ��m��
��m��
����m��![]() �������ABE�Ķ�����
�������ABE�Ķ�����
����![]() ��k������m��k����Ĺ�ϵʽ��
��k������m��k����Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0��
��1��������ABC����x��ԳƵ���A1B1C1��
��2����������ABC��ԭ��O����ʱ����ת90�����õ���A2B2C2��
��3����A1B1C1����A2B2C2����Գ�ͼ����������Գ�ͼ�Σ��������еĶԳ��
��4����A1B1C1����A2B2C2�����ĶԳ�ͼ�����������ĶԳ�ͼ�Σ�д�����еĶԳ����ĵ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
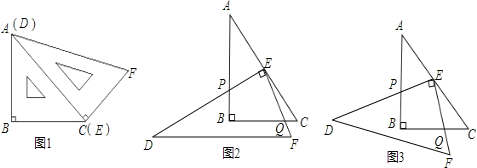
����Ŀ����ͼ1��һ��ֱ�����ǰ�����AB=BC��AC=DE����ABC=��DEF=90�㣬��EDF=30��
�����������ǰ�DEF��ֱ�Ƕ���E���������ǰ�ABC��б��AC�ϣ��ٽ����ǰ�DEF�Ƶ�E��ת����ʹ��DE���AB���ڵ�P����EF���BC�ڵ�Q��
̽��һ������ת�����У�
��1����ͼ2����![]() ʱ��EP��EQ����������������ϵ��������֤����
ʱ��EP��EQ����������������ϵ��������֤����
��2����ͼ3����![]() ʱ��EP��EQ����������������ϵ����˵�����ɣ�
ʱ��EP��EQ����������������ϵ����˵�����ɣ�
��3��������ԣ�1������2����̽���������д����![]() ʱ��EP��EQ�����������ϵʽΪ�� ��������m��ȡֵ��Χ���� ������ֱ��д�����ۣ�����֤����
ʱ��EP��EQ�����������ϵʽΪ�� ��������m��ȡֵ��Χ���� ������ֱ��д�����ۣ�����֤����
̽��������![]() ��AC=30cm������PQ������EPQ�����ΪS��cm2��������ת�����У�
��AC=30cm������PQ������EPQ�����ΪS��cm2��������ת�����У�
��1��S�Ƿ�������ֵ����Сֵ�������ڣ�������ֵ����Сֵ���������ڣ�˵�����ɣ�
��2������Sȡ��ͬ��ֵ����Ӧ��EPQ�ĸ�������Щ�仯�������ӦS��ֵ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ڣ�С�������ɽ������ɽ������ɽ���Ĺ����У���;��Ϣ��һ��ʱ�䣮������ɽ�ų���������ʱ��Ϊ![]() �����ӣ������ߵ�·��Ϊ
�����ӣ������ߵ�·��Ϊ![]() ���ף���
���ף���![]() ��
��![]() ֮��ĺ�����ϵ��ͼ��ʾ������˵��������ǣ� ��
֮��ĺ�����ϵ��ͼ��ʾ������˵��������ǣ� ��
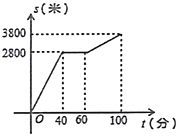
A.С����;��Ϣ����20����
B.С����Ϣǰ·����ʱ��ĺ�����ϵʽ![]()
C.С�����������������ߵ�·��Ϊ6600��
D.С����Ϣǰ��ɽ��ƽ���ٶȴ�����Ϣ����ɽ��ƽ���ٶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AE��BC��AF��CD������ֱ�ΪE��F����BE=DF��
��1����֤��ABCD�����Σ�
��2����AB=5��AC=6����ABCD�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com