
【题目】如图,点![]() 为
为![]() 的平分线上一点,
的平分线上一点,![]() 于
于![]() ,
,![]() ,求证:
,求证:![]() .
.
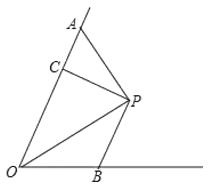
【答案】见解析.
【解析】
作PD⊥OB于D,根据角平分线的性质就可以得出PC=PD,根据HL可以判定Rt△PCO≌Rt△PDO,从而可得OC=OD,然后根据AAS得出△ACP≌△BDP,从而得到AC=BD,进而得出OA+OB=2OC.
证明:作PD⊥OB于D.
∴∠PDO=90°.
∵P为∠AOB的平分线上一点,PC⊥OA
∴PC=PD,∠PCA=90°.
∴∠PCA=∠PDO.
在Rt△PCO和Rt△PDO中,![]() ,
,
∴Rt△PCO≌Rt△PDO(HL),
∴OC=OD.
∵∠OBP+∠DBP=180°,且∠OAP+∠OBP=180°,
∴∠OAP=∠DBP.
在△ACP和△BDP中,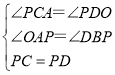 ,
,
∴△ACP≌△BDP(AAS),
∴AC=BD.
∴OA+OB=AC+OC+BO=BD+BO+OC=DO+OC=2OC.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
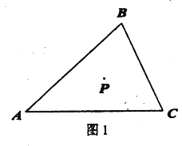
【题目】P是三角形![]() 内一点,射线PD//AC ,射线PB//AB .
内一点,射线PD//AC ,射线PB//AB .
(1)当点D,E分别在AB,BC 上时,
①补全图1:
②猜想![]() 与
与![]() 的数量关系,并证明;,
的数量关系,并证明;,
(2)当点![]() 都在线段
都在线段![]() 上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
上时,请先画出图形,想一想你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() ~
~![]() 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2![]() m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
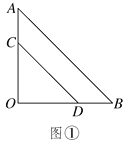
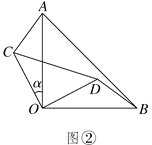
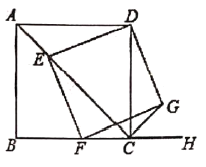
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
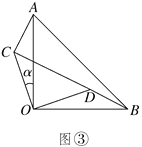
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为![]() ;设包装盒底面的长为
;设包装盒底面的长为![]() .
.
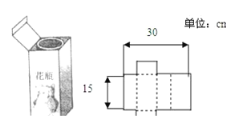
(1)用![]() 表示包装盒底面的宽;
表示包装盒底面的宽;
(2)用![]() 表示包装盒的表面积,并化简;
表示包装盒的表面积,并化简;
(3)若包装盒底面的长为![]() ,求包装盒的表面积.
,求包装盒的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
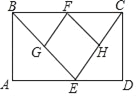
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形![]() 为正方形,
为正方形,![]() ,点
,点![]() 为对角线
为对角线![]() 上一动点,连接
上一动点,连接![]() ,过点
,过点![]() 作
作![]() .交
.交![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)求证:矩形![]() 是正方形;
是正方形;
(2)探究:![]() 的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com