
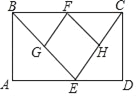
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
科目:初中数学 来源: 题型:
【题目】如图,![]() .
.

(1)如图①,在平面直角坐标系中,以![]() 为顶点,
为顶点,![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() ,若
,若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)如图②,![]() 为
为![]() 轴负半轴上一个动点,以
轴负半轴上一个动点,以![]() 为顶点,
为顶点,![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,当
点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,试问
轴负半轴向下运动时,试问![]() 的值是否发生变化?若不变,求其值,若变化,请说明理由;
的值是否发生变化?若不变,求其值,若变化,请说明理由;
(3)如图③,已知点![]() 坐标为
坐标为![]() ,
,![]() 是
是![]() 轴负半轴上一点,以
轴负半轴上一点,以![]() 为直角边作等腰
为直角边作等腰![]() ,
,![]() 点在
点在![]() 轴上,
轴上,![]() ,设
,设![]() 、
、![]() ,当
,当![]() 点在
点在![]() 轴的负半轴上沿负方向运动时,
轴的负半轴上沿负方向运动时,![]() 的和是否发生变化?若不变,求其值;若变化,请说明理由.
的和是否发生变化?若不变,求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
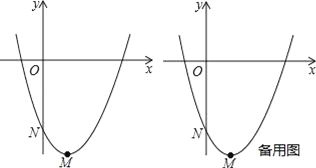
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
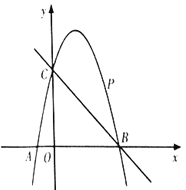
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
.点![]() 是直线
是直线![]() 上方的抛物线上一动点.
上方的抛物线上一动点.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,
,![]() ,并把
,并把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() .若四边形
.若四边形![]() 为菱形,请求出此时点
为菱形,请求出此时点![]() 的坐标;
的坐标;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的腰长为2,直角顶点A在直线l:y=2x+2上移动,且斜边BC∥x轴,当△ABC在直线l上移动时,BC的中点D满足的函数关系式为( )

A. y=2x B. y=2x+1 C. y=2x+2﹣![]() D. y=2x﹣
D. y=2x﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
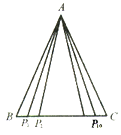
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂
直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=![]() ,BC=9,则DF等于( )
,BC=9,则DF等于( )

A. ![]() B.
B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com