
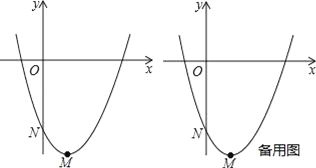
����Ŀ����֪������l��y=ax2+bx+c��a��b��c����Ϊ0���Ķ���ΪM����y��Ľ���ΪN�����dz���NΪ���㣬�Գ�����y���ҹ���M��������Ϊ������l�����������ߣ�ֱ��MNΪ������l������ֱ�ߣ�
��1����ͼ��������y=x2��2x��3�����������ߵĽ���ʽ���� ��������ֱ�ߵĽ���ʽ���� ����
��2����һ�������ߵ����������ߺ�����ֱ�߷ֱ���y=��2x2+1��y=��2x+1�������������ߵĽ���ʽ��
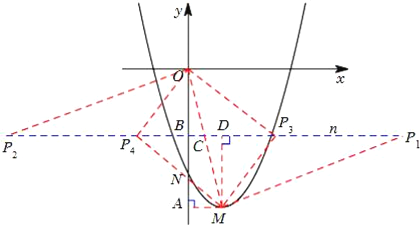
��3����ͼ���裨1���е�������y=x2��2x��3�Ķ���ΪM����y�ύ��ΪN������������ֱ��MN���Ƶ�N��ת����x��ƽ�У�����y������ƽ��1����λ��ֱ��n��P��ֱ��n�ϵĶ��㣬�Ƿ���ڵ�P��ʹ��POMΪֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2��3, y=��x��3����2��y=2x2��4x+1��
��3�����ڣ�PΪ��![]() ����2����
����2����![]() ����2����9����2����8����2����
����2����9����2����8����2����
����������������1�����������߶���Ϊԭ��������y��Ľ��㣬��ɸ��ݶ����趥��ʽ���̣������������߹�ԭ�����ߵĶ��������ʽ����MN����ʽ����
��2����֪���������ߺ�����ֱ����ԭ������˼·�����루1���෴����������������������ֱ�ߵ�������ֱ�Ϊ������������ԭ�����ߵĽ��㣬����Ƶ�ԭ�����߶���ʽ���ٴ��뾭���㣬���ý���ʽ����3����N��0����3��������ֱ��MN�Ƶ�N��ת����x��ƽ�еõ�y=��3��������ƽ��1����λ����ֱ��y=��2������P����裨x����2����������ϵ��ʹ�á�POMΪֱ��������һ�㿼�ǹ��ɶ�������������ϵ�е����㣬�ֱ������ƽ����x�ᡢy���ֱ�ߣ���ɹ�������������Ϊб�ߵ�ֱ�������Σ���ֱ�DZ߳���Ϊ������������ľ���ֵ���������ǿ���������������������ߵ�ƽ����Ȼ����Ϲ������㹴�ɶ����������������P�����꣮
���������
��1����������y=x2��2x��3����0����3����
����������������Ϊy=ax2��3��
��y=x2��2x��3=x2��2x+1��4=��x��1��2��4��
������������Ϊy=ax2��3��������y=x2��2x��3�Ķ��㣨1����4����
�ੁ4=a1��3��
��� a=��1��
������������Ϊy=��x2��3��
������ֱ��Ϊy=kx+b��
��y=kx+b����0����3������1����4����
��![]() ��
��
��![]() ��
��
������ֱ��Ϊy=��x��3��
��2�������������ߺ�����ֱ��������ֱ�Ϊԭ�����������������ߵĶ��㣬
�ཫy=��2x2+1��y=��2x+1��������![]() ��
��
��� ![]() ��
��![]() ��
��
������������y=��2x2+1�Ķ���Ϊ��0��1����
��ԭ�����ߵĶ���Ϊ��1����1����
��ԭ������Ϊy=a��x��1��2��1��
��y=a��x��1��2��1����0��1����
��1=a��0��1��2��1��
��� a=2��
��ԭ������Ϊy=2x2��4x+1��
��3����N��0����3����
��MN�Ƶ�N��ת����x��ƽ�к���ʽΪy=��3��
������y������ƽ��1����λ�õ�ֱ��n����ʽΪy=��2��
���P������x����2����
��O��0��0����M��1����4����
��OM2=��xM��xO��2+��yO��yM��2=1+16=17��
OP2=��|xP��xO|��2+��yO��yP��2=x2+4��
MP2=��|xP��xM|��2+��yP��yM��2=��x��1��2+4=x2��2x+5��
�ٵ�OM2=OP2+MP2ʱ����17=x2+4+x2��2x+5��
���x=![]() ��x=
��x=![]() ����P��
����P��![]() ����2����P��
����2����P��![]() ����2����
����2����
�ڵ�OP2=OM2+MP2ʱ����x2+4=17+x2��2x+5��
��� x=9����P��9����2����
�۵�MP2=OP2+OM2ʱ����x2��2x+5=x2+4+17��
��� x=��8����P����8����2����
������������P��![]() ����2����
����2����![]() ����2����9����2����8����2��ʱ����POMΪֱ�������Σ�
����2����9����2����8����2��ʱ����POMΪֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���εο쳵��һ�ֱ�ݵij��й��ߣ��Ƽ۹������±���
�Ʒ���Ŀ | ��̷� | ʱ���� | Զ;�� |
���� | 1.8Ԫ/���� | 0.45Ԫ/���� | 0.4Ԫ/���� |
ע����������̷ѡ�ʱ���ѡ�Զ;�������ֹ��ɣ�������̷Ѱ��г���ʵ����̼��㣻ʱ���Ѱ��г���ʵ��ʱ����㣻Զ;�ѵ���ȡ��ʽΪ���г����10��������(��10����)����Զ;�ѣ�����10����ģ���������ÿ������0.4Ԫ. | |||
(1)��С�������εο쳵���г����Ϊ20����г�ʱ��Ϊ30���ӣ����踶����________Ԫ��
(2)��С�������εο쳵���г����Ϊa����г�ʱ��Ϊb���ӣ���С��Ӧ�����Ѷ���Ԫ(�ú�a��b�Ĵ���ʽ��ʾ��������.)
(3)С����С�Ÿ��Գ����εο쳵���г���̷ֱ�Ϊ9.5������14.5�������³�ʱ��������������ͬ����ô�������εο쳵���г�ʱ�������ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Բ��DEC����ֱ��BP���ڵ�ˮƽ��������BP��Բ����Բ��Բ����Բ�ĸ�Ϊ2![]() m������뾶Ϊ2 m��ij��Դλ�ڵ�A��������Բ����ˮƽ�������µ�Ӱ��BE��4 m.
m������뾶Ϊ2 m��ij��Դλ�ڵ�A��������Բ����ˮƽ�������µ�Ӱ��BE��4 m.
(1)���ABC�Ķ�����
(2)����ACP��2��ABC�����ԴA��ˮƽ��ĸ߶ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
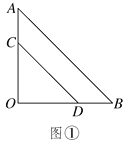
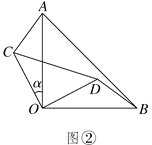
����Ŀ���������ֱ��������ֽƬAOB��COD��ͼ����ʾ���ã�ֱ�Ƕ����غ��ڵ�O����AB��25.����ֽƬAOB��������ֽƬCOD�Ƶ�O��ʱ����ת��(0��������90��)�Ƕȣ���ͼ����ʾ��
(1)��ͼ���У���֤��AC��BD����AC��BD��
(2)��BD��CD��ͬһֱ����(��ͼ��)ʱ����AC��7����CD�ij���
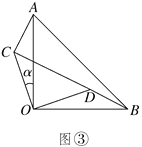
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����ϰ�װ�м�������ƽ��ֽ����ͼ��ʾ����װ�еĸ�Ϊ![]() �����װ�е���ij�Ϊ
�����װ�е���ij�Ϊ![]() ��
��
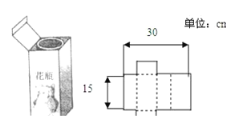
��1����![]() ��ʾ��װ�е���Ŀ���
��ʾ��װ�е���Ŀ���
��2����![]() ��ʾ��װ�еı������������
��ʾ��װ�еı������������
��3������װ�е���ij�Ϊ![]() �����װ�еı������
�����װ�еı������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������P��AB�·��İ�Բ�ϲ����A��B�غϵ�һ�����㣬��CΪAP�е㣬�ӳ�CO����O�ڵ�D������AD������D����O�����߽�PB��͢�����ڵ�E����CE��AB�ڵ�F������DF��
��1����֤����DAC�ա�ECP��
��2����գ�
���ı���ACED�Ǻ���������ı��Σ�
���ڵ�P�˶������У��߶�DF��AP��������ϵ���� ����
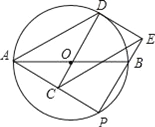
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD�У�E��AD���ϵ�һ�����㣬��F��G��H�ֱ���BC��BE��CE���е㣮
��1����֤����BGF�ա�FHC��
��2����AD=a�����ı���EGFH��������ʱ�������ABCD�������
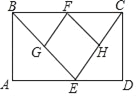
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4cm��BC=8cm������ABC�ضԽ���AC�۵����õ���AB'C��B'C��AD�ཻ�ڵ�E����AE�ij�________��
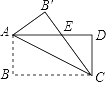
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϵĵ㣬����
�ϵĵ㣬����![]() �ܳ���Сʱ��
�ܳ���Сʱ��![]() �Ķ���Ϊ�� ��
�Ķ���Ϊ�� ��
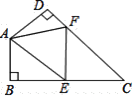
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com