
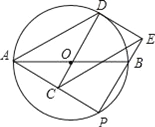
【题目】如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.
(1)求证:△DAC≌△ECP;
(2)填空:
①四边形ACED是何种特殊的四边形?
②在点P运动过程中,线段DF、AP的数量关系是 .
【答案】(1)证明见解析;(2)①四边形ACED是平行四边形;②DF=![]() AP,
AP,
【解析】
(1)由已知条件易得∠CDE=∠DCA=∠DCP=∠P=90°,由此可得四边形DCPE是矩形,从而可得DC=EP,这样结合AC=PC即可由“SAS”证得△DAC≌△ECP;
(2)①由(1)中所得△DAC≌△ECP可得AD=CE,∠DAC=∠ECP,从而可得AD∥CE,由此即可得到四边形ACED是平行四边形;②由OA=OD,AD∥CE易得∠DAO=∠ADC=∠DCF,由此可得A、C、F、D四点共圆,结合∠DAF=∠ADC可得在该圆中弦DF=AC,结合点C是AP的中点即可得到DF=![]() AP.
AP.
(1)∵DE为切线,
∴OD⊥DE,
∴∠CDE=90°,
∵点C为AP的中点,
∴DC⊥AP,
∴∠DCA=∠DCP=90°,
∵AB是⊙O直径,
∴∠APB=90°,
∴四边形DEPC为矩形,
∴DC=EP,
∵在△DAC和△ECP中: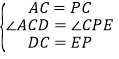 ,
,
∴△DAC≌△ECP;
(2)①∵△DAC≌△ECP,
∴AD=CE,∠DAC=∠ECP,
∴AD∥CE,
∴四边形ACED是平行四边形;
②∵OA=OD,
∴∠DAF=∠ADC,
∵AD∥CE,
∴∠ADC=∠DCF,
∴∠DAF=∠DCF,
∴A,C,F,D四点共圆,
又∵∠ADF=∠ADC,
∴AC=DF,
∵AC=![]() AP,
AP,
∴DF=![]() AP.
AP.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
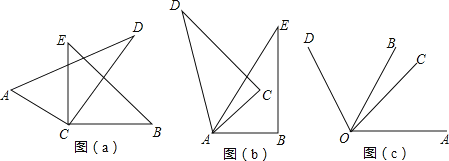
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
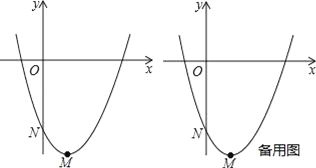
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按![]() ,
,![]() ,
,![]() ,
,![]() 四个等级进行统计,制成了如下不完整的统计图.(说明:
四个等级进行统计,制成了如下不完整的统计图.(说明:![]() 级:8分—10分,
级:8分—10分,![]() 级:7分—7.9分,
级:7分—7.9分,![]() 级:6分—6.9分,
级:6分—6.9分,![]() 级:1分—5.9分)
级:1分—5.9分)
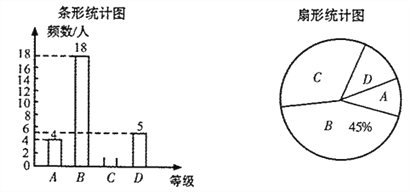
根据所给信息,解答以下问题:
(1)在扇形统计图中,![]() 对应的扇形的圆心角是_______度;
对应的扇形的圆心角是_______度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在_______等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
.点![]() 是直线
是直线![]() 上方的抛物线上一动点.
上方的抛物线上一动点.
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,
,![]() ,并把
,并把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() .若四边形
.若四边形![]() 为菱形,请求出此时点
为菱形,请求出此时点![]() 的坐标;
的坐标;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
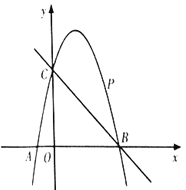
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
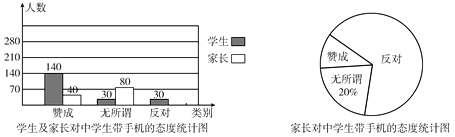
【题目】“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com