
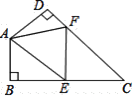
【题目】在四边形![]() 中
中![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,当△
上的点,当△![]() 周长最小时,
周长最小时,![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
要使△AEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′E+∠A″=∠HAA′=55°,进而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,

∵∠C=55°,
∴∠DAB=125°,
∴∠HAA′=55°,
∴∠AA′E+∠A″=∠HAA′=55°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=55°,
∴∠EAF=125°-55°=70°.
故选:B.


科目:初中数学 来源: 题型:
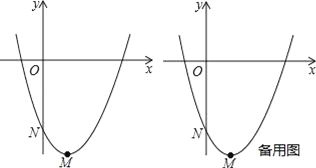
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
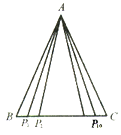
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆大巴车在一条南北方向的道路上来回运送旅客,某一天早晨该车从A地出发,晚上到达B地,预定向北为正方向,当天行驶记录如下(单位:千米)+18,-9,+7,-14,-6,+13,-6,-8 请你根据计算回答下列问题:
(1)B地在A地何方?相距多少千米?
(2)该车这一天共行驶多少千米?
(3)若该车每千米耗油0.5升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
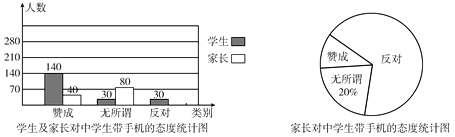
【题目】“校园手机”现象越来越受到社会的关注,“六一”期间,记者随机调查了某校若干名初四学生和家长对中学生带手机现象的看法,统计整理并制作了如下两幅统计图.
(1)求这次调查的家长人数,并补全条形图;
(2)求扇形图中表示家长“赞成”的圆心角的度数;
(3)若南岗区共有初四学生10000名,请估计在这些学生中,对中学生带手机现象持“无所谓”态度的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=45°,AB的垂直平分线交AB于点E,交BC于点D;AC的垂
直平分线交AC于点G,交BC与点F,连接AD、AF,若AC=![]() ,BC=9,则DF等于( )
,BC=9,则DF等于( )

A. ![]() B.
B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
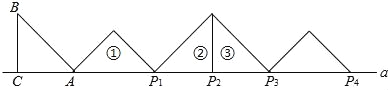
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=![]() +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=![]() +2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
+2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com