
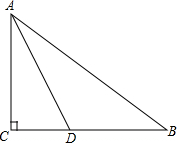
 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB,交BC于点D,求CD.
如图,在△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB,交BC于点D,求CD. 分析 过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得CD=DE,利用勾股定理列式求出AB,然后根据S△ABC=S△ACD+S△ABD列方程求解即可.
解答 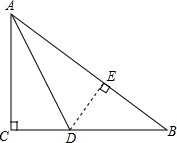 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵∠ACB=90°,AD平分∠CAB,
∴CD=DE,
由勾股定理得,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵S△ABC=S△ACD+S△ABD,
∴$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AC×CD+$\frac{1}{2}$×AB×DE,
即$\frac{1}{2}$6×8=$\frac{1}{2}$×6×CD+$\frac{1}{2}$×10×CD,
解得CD=3.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,勾股定理,熟记性质并作辅助线是解题的关键,利用三角形的面积列出方程求解更简便.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
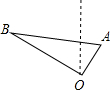 如图所示,甲、乙两轮船于上午8时同时从码头O分别向北偏东32°和北偏西58°的方向出发,甲轮船的速度为30海里/时,乙轮船的速度为40海里/时,则下午1时两轮船相距多少海里?
如图所示,甲、乙两轮船于上午8时同时从码头O分别向北偏东32°和北偏西58°的方向出发,甲轮船的速度为30海里/时,乙轮船的速度为40海里/时,则下午1时两轮船相距多少海里?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 制作桌面 | 制作桌脚 | |
| 1立方米木材 | ||
| X立方米木材 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
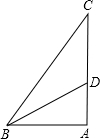 如图,在Rt△ABC中,∠CAB=90°,sinC=$\frac{3}{5}$,AC=6,BD平分∠CBA交AC边于点D.求:
如图,在Rt△ABC中,∠CAB=90°,sinC=$\frac{3}{5}$,AC=6,BD平分∠CBA交AC边于点D.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com