
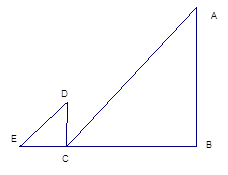
 的中位线,M是DE的中点, CM的延长线交AB于N,那么
的中位线,M是DE的中点, CM的延长线交AB于N,那么 =_________________.
=_________________.
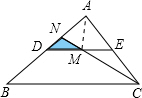 解:DE是中位线,所以S△ADE=
解:DE是中位线,所以S△ADE= S△ABC,
S△ABC, S△ABC,连接AM,AE=CE,所以S△AEM=S△MEC
S△ABC,连接AM,AE=CE,所以S△AEM=S△MEC ×
× S△ABC=
S△ABC=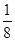 S△ABC,所以S四边形DBCM=(
S△ABC,所以S四边形DBCM=( -
-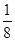 )S△ABC=
)S△ABC=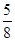 S△ABC,
S△ABC,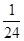 S△ABC
S△ABC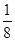 -
-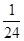 )S△ABC=
)S△ABC=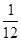 S△ABCS四边形ANME=(
S△ABCS四边形ANME=(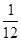 +
+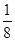 )S△ABC=
)S△ABC=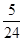 S△ABC
S△ABC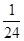 :
: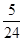 =1:5.
=1:5. S△ABC,便可找到突破口解答.
S△ABC,便可找到突破口解答.

科目:初中数学 来源:不详 题型:解答题
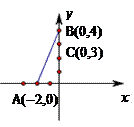
 0,4)、B(2,4),它的最高点纵坐标为
0,4)、B(2,4),它的最高点纵坐标为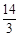 ,点P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
,点P是第一象限抛物线上一点且PA=PO,过点P的直线分别交射线AB、x正半轴于C、D.设AC=m,OD=n.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.60 | B.32 | C.48 | D.50 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
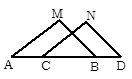
| A.∠M=∠N | B.AM∥CN |
| C.AB=CD | D.AM=CN |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.7 | B.8 | C.9 | D.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com