
����Ŀ������������ʵ��a ��b ����![]() ����
����![]() ��
��
��![]() ��ֻ��a=bʱ���Ⱥų�����
��ֻ��a=bʱ���Ⱥų�����
���ۣ���![]() (
(![]() ��Ϊ��ʵ��)�У���
��Ϊ��ʵ��)�У���![]() Ϊ��ֵp����
Ϊ��ֵp����![]() ��ֻ�е�a=bʱ��
��ֻ�е�a=bʱ��![]() ����Сֵ
����Сֵ![]() ��
��
�����������ݣ��ش��������⣺
��1����n��0��ֻ�е�n= ______ʱ��![]() ����Сֵ��
����Сֵ��
��2������һ��ͼ����4��ȫ�ȵľ���Χ�ɵĴ������Σ��пղ�����С�����Σ����εij��Ϳ��ֱ�Ϊa��b �������ô����������ĸ����ε�����Ĵ�С��ϵ����֤![]() ����ָ���Ⱥų���ʱ��������
����ָ���Ⱥų���ʱ��������
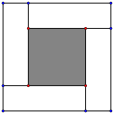
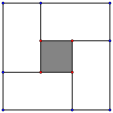
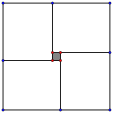 ......
......
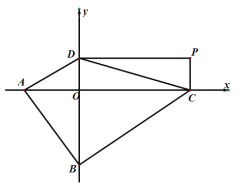
��3������ͼ����֪A(��3��0)��B(0����4)����P�ǵ�һ�����ڵ�һ�����㣬��P���������������ߣ��ֱ�![]() ���
���![]() ����C��D���㣬����OCPD�����ʼ��Ϊ12�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
����C��D���㣬����OCPD�����ʼ��Ϊ12�����ı���ABCD�������Сֵ����˵����ʱ�ı���ABCD����״��
���𰸡���1��1�� ��2��![]() ������������3��S�ı���ABCD=24Ϊ�����Сֵ���ı���ABCDΪ����.
������������3��S�ı���ABCD=24Ϊ�����Сֵ���ı���ABCDΪ����.
��������
��1�����Ķ����ϣ���֪��![]() ʱ��
ʱ��![]() ����Сֵ��
����Сֵ��
��2�����ݴ������ε�������ڵ����ĸ����ε����֮�ͼ��ɽ��.
��3����![]() �����ݾ���OCPD�����ʼ��Ϊ12�ɵ�xy=12���ٸ��ݶԽ����ഹֱ���ı��ε���������Լ�����ĵ�P���������õ���Ӧ���ۣ�
�����ݾ���OCPD�����ʼ��Ϊ12�ɵ�xy=12���ٸ��ݶԽ����ഹֱ���ı��ε���������Լ�����ĵ�P���������õ���Ӧ���ۣ�
��1����n��0��ֻ�е�n= _1___ʱ��![]() ����Сֵ��
����Сֵ��
��2���١�![]() ��
�� ![]()
��ͼ��![]() ����
����![]() ��
��![]() ��
��
����![]() ����P�ڵ�һ���ޣ���
����P�ڵ�һ���ޣ���![]()
��![]()
![]()
![]()
��![]()
��![]()
��![]()
��![]() ����
����![]()
��![]()
�൱�ҽ���![]() ʱ����x=3ʱ��
ʱ����x=3ʱ��![]() Ϊ�����Сֵ
Ϊ�����Сֵ
��![]() ��
��
��![]()
����![]()
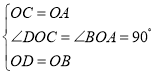
��![]()
��![]()
��![]()
���ı���ABCD��ƽ���ı���
��AC��BD
���ı���ABCD������


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ�����˶��ѳ�Ϊһ��ʱ�� ��Ϊ�˽�����о������˶��������ij�����ݵĹ�����Ա��չ��һ���ʾ����飬�ʾ����ݰ��������Ŀ:
A:�������˶���B:���㳡�裻C:�μӱ����ţ�D:ɢ����E:���˶�.
�����Ǹ��ݵ��������Ƶ�ͳ��ͼ����һ���֣�
�˶���ʽ | A | B | C | D | E |
���� |
|
|
|
|
|
�������������Ϣ���ش���������:
![]() �����ʾ�����Ĺ��� �ˣ�ͼ���е�
�����ʾ�����Ĺ��� �ˣ�ͼ���е�![]() ��
��![]() .
.
![]() ͳ��ͼ�У�
ͳ��ͼ�У�![]() ������Ӧ�����ε�Բ�ĽǵĶ����� ��.
������Ӧ�����ε�Բ�ĽǵĶ����� ��.

![]() �����л���·������ϲ�����˶�����֮һ��ÿ�춼�С������š������ij����Լ��
�����л���·������ϲ�����˶�����֮һ��ÿ�춼�С������š������ij����Լ��![]() �ˣ��������һ�¸������μӻ���·�������š�������.
�ˣ��������һ�¸������μӻ���·�������š�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��λͬѧ�ڻ���![]() ʱ�Ľ��������£�
ʱ�Ľ��������£�![]()
![]()
Aͬѧ��ԭʽ=![]() ����һ����
����һ����
=![]() ���ڶ�����
���ڶ�����
=![]() ����������
����������
Bͬѧ��ԭʽ=![]() ����һ����
����һ����
=![]() ���ڶ�����
���ڶ�����
=![]() ����������
����������
��1�������ж���λͬѧ�Ľ�������ȷ��
A��_____ ��B��______ (��ȷ�Ĵ���������Ĵ���)
���ڳ�����ͬѧ����ָ�����Ǵӵڼ�����ʼ�����ģ������ԭ����ʲô��
��2��������ڣ�1�����ж���λͬѧ�Ľ���Ǵ���ģ���д������Ϊ��ȷ�Ľ����̣��������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�![]() ��EΪCD�ߵ��е㣬��
��EΪCD�ߵ��е㣬��![]() �Ƶ�E˳ʱ����ת
�Ƶ�E˳ʱ����ת![]() ����D�Ķ�Ӧ��ΪC����A�Ķ�Ӧ��ΪF������E��
����D�Ķ�Ӧ��ΪC����A�Ķ�Ӧ��ΪF������E��![]() ��BC�ڵ�M������AM��BD���ڵ�N���������н��ۣ�
��BC�ڵ�M������AM��BD���ڵ�N���������н��ۣ�![]() ��
��![]() ��
��![]() ��
��![]() ��NΪ
��NΪ![]() �����ģ�������ȷ�ĸ���Ϊ
�����ģ�������ȷ�ĸ���Ϊ![]() ����
����![]()
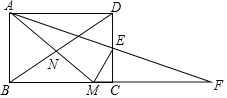
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������![]() ��ͼ��������
��ͼ��������
(1)����![]() ���Ա���x��ȡֵ��Χ��___��
���Ա���x��ȡֵ��Χ��___��
(2)�����ĸ�����ͼ����,����![]() ��ͼ�������___��
��ͼ�������___��
A��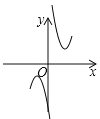 B.
B.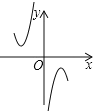 C.
C.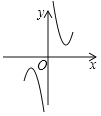 D.
D.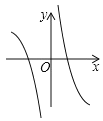
(3)���ں���![]() ����
����![]() ʱ��y��ȡֵ��Χ��
ʱ��y��ȡֵ��Χ��
�뽫������������Ĺ��̲���������
�⣺��x>0
��![]()
=![]()
��![]()
��y=____.
����չӦ�ã�
(4)������![]() ����y��ȡֵ��Χ.
����y��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
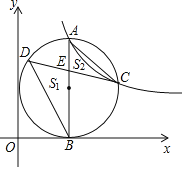
����Ŀ����ͼ����A�Ƿ���������![]() ͼ���һ������һ�㣬����A��
ͼ���һ������һ�㣬����A��![]() ����B�㣬��ABΪֱ����Բǡ����y�����У�������������ͼ���ڵ�C����AB������Բ����һ����D������CD��AB�ڵ�
����B�㣬��ABΪֱ����Բǡ����y�����У�������������ͼ���ڵ�C����AB������Բ����һ����D������CD��AB�ڵ�![]() ��
��![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ������BC����
������BC����![]() ��______��������
��______�����Σ���![]() ��ֵ���Ϊ1����k��ֵΪ______��
��ֵ���Ϊ1����k��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ĵ����ϣ������ɸ��ⳤ��ȫ��ͬ��С��������һ��������.

��1���뻭����������������ͼ������ͼ����ͼ�����ú�ɫīˮ��ڣ���
��2�������������ͼ������ͼ���䣬��ô��������������������� ��С�����壿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����и�ʽ
��x��1����x+1����x2��1
��x��1����x2+x+1����x3��1
��x��1����x3+x2+x+1����x4��1
��1���������Ϲ��ɣ���x��1����x6+x5+x4+x3+x2+x+1������ ����
��2�����ܷ��ɴ˹��ɳ�һ����ɣ�x��1����xn+xn��1+����+x+1������ ����
��3���������Ϲ�����32018+32017+32016+��32+3+1�Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A ���Ӧ����Ϊ��5��B ����A ���ұߣ��������ϼס�����B�ֱ���2����λ/�롢1����λ/����ٶ������˶����������ϱ���A ��3����λ/����ٶ������˶���
��1�����������ϱ�����5���˶���C �㣬��C ���ʾ������
![]()
��2��������ͬʱ������������������1�������ң���B ���ʾ������
![]()
��3���ڣ�2���������£�������ͬʱ������ʱ��Ϊt �룬�Ƿ����t��ֵ��ʹ�����ҵľ����DZ����ľ����2���������ڣ����t ֵ���������ڣ�˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com