
【题目】如图,在矩形ABCD中,![]() ,E为CD边的中点,将
,E为CD边的中点,将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,点D的对应点为C,点A的对应点为F,过点E作
,点D的对应点为C,点A的对应点为F,过点E作![]() 交BC于点M,连接AM、BD交于点N,现有下列结论:
交BC于点M,连接AM、BD交于点N,现有下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 点N为
点N为![]() 的外心.其中正确的个数为
的外心.其中正确的个数为![]()
![]()
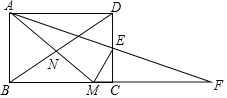
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】分析:
(1)由旋转的性质易得AD=FC,AE=FE,结合ME⊥AF可得AM=MF,结合MF=MC+CF即可得到结论①成立;(2)假设AM=DE+BM成立,则结合(1)可推得CE=2MC,但由题中条件不能得到CE=2MC一定成立,故结论②不成立;(3)由已知条件证△ADE∽△ECM,结合DE=CE即可证得结论③成立;(4)过点M作MF⊥AD于点F,连接BF交AM于点Q,则易证点Q是AM的中点,由此可得点N不是AM的中点,从而可得结论④不成立;综合(1)--(4)即可得到所求答案.
详解:
(1)∵△CEF是由△DEA绕点E旋转180°得到的,
∴AD=FC,AE=FE,DE=CE,
又∵ME⊥AF,
∴AM=MF,
∵MF=MC+CF,
∴AM=AD+MC,即结论①成立;
(2)假设AM=DE+BM成立,
∵由(1)可知AM=AD+MC,
∴AD+MC=DE+BM,
又∵AD=BC=BM+MC,DE=CE,
∴BM+MC+MC=BM+CE,
∴2MC=CE,
∵由题中条件不能确定CE=2MC成立,
∴AM=DE+BM不一定成立,故结论②不成立;
(3)∵ME⊥AF,四边形ABCD是矩形,
∴∠ADE=∠MEF=∠ECM=90°,
∴∠MEC+∠EMC=90°,∠EMC+∠F=90°,
∴∠MEC=∠F,
∵AD∥BC,
∴∠DAE=∠F,
∴∠DAE=∠MEC,
∴△ADE∽△ECM,
∴AD:EC=DE:CM,
∴EC·DE=AD·CM,
又∵EC=DE,
∴DE2=AD·CM,故结论③成立;
(4)如下图,过点M作MF⊥AD于点F,连接BF交AM于点Q,
∴∠ABM=∠BAF=∠AFM=90°,
∴四边形ABMF是矩形,
∴点Q是AM的中点,
∴点Q是△ABM的外心,
∵点Q与点N不重合,
∴点N不是△ABM的外心,故结论④不成立.
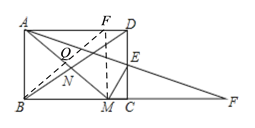
综上所述,上述4个结论中,成立的是①③,共2个.
故选B.


科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将检查结果绘制成下面两个统计图.
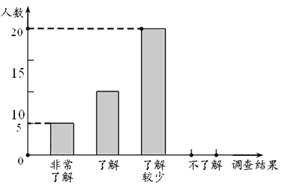

⑴ 本次调查的学生共有 人,“了解较少”的学生人数所占的百分比为 ;
⑵ 补全条形统计图;
⑶ 若该校共有1300名学生,请根据统计结果估算该校“不了解”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发公司生产的960件新产品需要精加工后才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的![]() ,甲、乙两个工厂每天各能加工多少个新产品?
,甲、乙两个工厂每天各能加工多少个新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:﹣(﹣2),-3,![]() ,﹣0.101001,﹣|﹣2|,
,﹣0.101001,﹣|﹣2|,![]() ,0.2020020002…,
,0.2020020002…,![]() ,-
,-![]() ,0.
,0.
负整数集合:{____________…}.
负分数集合:{____________…}.
无理数集合:{____________…}.
非负数集合:{____________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)如图1,在边长为x的正方形内剪去边长为y的小正方形,剩下的图形面积可以表示为 ;把剩下的这个图形沿图2的虚线剪开,并拼成图3的长方形,可得长为 、宽为 ,那么这个长方形的面积可以表示为 ,不同的方法求得的面积应相等,由此可以得到一个等式.
(数学应用)利用得到的等式解决以下问题:
(1)![]()
(2)![]()
(思维拓展)(3)利用得到的等式计算![]() …
…![]()
解:原式=![]() …
…![]()
请你把接下来的计算过程补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意正实数a ,b ,∵![]() ,∴
,∴![]() ,
,
∴![]() ,只有a=b时,等号成立.
,只有a=b时,等号成立.
结论:在![]() (
(![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值p,则
为定值p,则![]() ,只有当a=b时,
,只有当a=b时,![]() 有最小值
有最小值![]() .
.
根据上述内容,回答下列问题:
(1)若n>0,只有当n= ______时,![]() 有最小值;
有最小值;
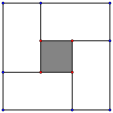
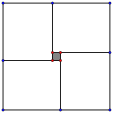
(2)下面一组图是由4个全等的矩形围成的大正方形,中空部分是小正方形,矩形的长和宽分别为a,b ,试利用大正方形与四个矩形的面积的大小关系,验证![]() ,并指出等号成立时的条件;
,并指出等号成立时的条件;
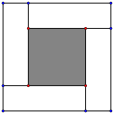
 ......
......
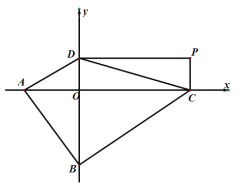
(3)如下图,已知A(-3,0),B(0,-4),点P是第一象限内的一个动点,过P点向坐标轴作垂线,分别交![]() 轴和
轴和![]() 轴于C,D两点,矩形OCPD的面积始终为12,求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
轴于C,D两点,矩形OCPD的面积始终为12,求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长和为______.(n≥2,且n为整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com