练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某开发公司生产的960件新产品需要精加工后才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的，甲、乙两个工厂每天各能加工多少个新产品?

    【答案】甲、乙两个工厂每天各能加工16个、24个新产品

    【解析】

    设乙每天加工新产品x件，则甲每天加工新产品 x件，甲单独加工完这批产品需 天，乙单独加工完这批产品需 天，根据题意找出等量关系：甲厂单独加工这批产品所需天数-乙工厂单独加工完这批产品所需天数=20，由等量关系列出方程求解．

    设乙每天加工新产品x件,则甲每天加工新产品x件，

    根据题意得=20，

    解得x=24，

    经检验，x=24符合题意，

    则x=24×=16，

    所以甲、乙两个工厂每天各能加工16个、24个新产品；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，任意四边形ABCD，对角线AC、BD交于O点，过各顶点分别作对角线AC、BD的平行线，四条平行线围成一个四边形EFGH．试想当四边形ABCD的形状发生改变时，四边形EFGH的形状会有哪些变化？完成以下题目：

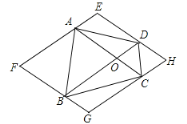
    (1)①当ABCD为任意四边形时，四边形EFGH为___________；

    ②当四边形ABCD为矩形时，四边形EFGH为___________；

    ③当四边形ABCD为菱形时，四边形EFGH为___________；

    ④当四边形ABCD为正方形时，四边形EFGH为___________；

    (2)请对(1)中①③你所写的结论进行证明

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在中，动点在边上，以每秒的速度从点向点运动．

    （1）如图1，在运动过程中，若平分，且满足，求的度数．

    （2）如图2，在（1）的条件下，连结并延长与的延长线交于点，连结，若，求的面积．

    （3）如图3，另一动点在边上，以每秒的速度从点出发，在间往返运动，两点同时出发，当点到达点时停止运动(同时点也停止)，若，求当运动时间为多少秒时，以D，四点组成的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点C与某建筑物底端B相距306米（点C与点B在同一水平面上），某同学从点C出发，沿同一剖面的斜坡CD行走195米至坡顶D处，斜坡CD的坡度（或坡比）i=1：2.4，在D处测得该建筑物顶端A的俯角为20°，则建筑物AB的高度约为（精确到0.1米，参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364）（ ）

    A.29.1米
    B.31.9米
    C.45.9米
    D.95.9米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：点A在射线CE上，∠C＝∠D．

    ⑴如图1，若AD∥BC，求证：BD∥AC；

    ⑵如图2，若∠BAC＝∠BAD，BD⊥BC，请探究∠DAE与∠C的数量关系，写出你的探究结论，并加以证明；

    ⑶如图3，在⑵的条件下，过点D作DF∥BC交射线于点F，当∠DFE＝8∠DAE时，求∠BAD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
    ①4ac＜b2；
    ②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；
    ③3a+c＞0
    ④当y＞0时，x的取值范围是﹣1≤x＜3
    ⑤当x＜0时，y随x增大而增大
    其中结论正确的个数是（ ）

    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点，，，点是三角形边上任意一点，三角形经过平移后得到三角形，点的对应点为.

    （1）直接写出点的坐标______________.

    （2）画出三角形平移后的三角形.

    （3）在轴上是否存在一点，使三角形的面积等于三角形面积的，若存在，请求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：

    （1）九（1）班的学生人数为__ ， 并把条形统计图补充完整；
    （2）扇形统计图中m=10 ， n=20 ， 表示“足球”的扇形的圆心角是多少度；
    （3）排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如何求tan75°的值？按下列方法作图可解决问题，如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BM上截取线段BD，使BD=AB，连接AD，依据此图可求得tan75°的值为（ ）

    A.2
    B.2+
    C.1+
    D.

    查看答案和解析>>

    同步练习册答案