
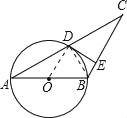
【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,根据三角形中位线定理得出OD∥BC,由DE⊥BC得出OD⊥DE,根据切线的判定定理即可得出结论;
(2)先证明Rt△CDB∽Rt△CED,然后根据相似三角形的对应边成比例求出BC的长,最后根据三角形的中位线定理即可求出圆的半径.
试题解析:
(1)证明:连接OD;
∵AD=CD,AO=BO,
∴OD∥BC.
∵DE⊥BC,
∴OD⊥DE.
∴DE与⊙O相切.
(2)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
∴∠BDC=90°,
又∵DE⊥BC,
Rt△CDB∽Rt△CED,
∴![]() =
=![]() ,
,
∴BC=![]() =
=![]()
又∵OD=![]() BC,
BC,
∴OD=![]() ×
×![]() =
=![]() ,
,
即⊙O的半径为![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC与BD相交于点O,且OA=OB,OC=OD,AD=BC,则图中共有全等三角形( )

A. 4对B. 3对C. 2对D. 1对
查看答案和解析>>
科目:初中数学 来源: 题型:
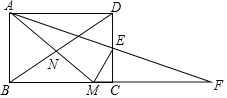
【题目】如图,在矩形ABCD中,![]() ,E为CD边的中点,将
,E为CD边的中点,将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,点D的对应点为C,点A的对应点为F,过点E作
,点D的对应点为C,点A的对应点为F,过点E作![]() 交BC于点M,连接AM、BD交于点N,现有下列结论:
交BC于点M,连接AM、BD交于点N,现有下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 点N为
点N为![]() 的外心.其中正确的个数为
的外心.其中正确的个数为![]()
![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
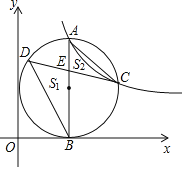
【题目】如图,点A是反比例函数![]() 图象第一象限上一点,过点A作
图象第一象限上一点,过点A作![]() 轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点
轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点![]() 记
记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接BC,则
,连接BC,则![]() 是______三角形,若
是______三角形,若![]() 的值最大为1,则k的值为______.
的值最大为1,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,由若干个棱长完全相同的小正方体搭成一个几何体.

(1)请画出这个几何体的主视图和左视图(作图必须用黑色墨水描黑);
(2)如果保持主视图和左视图不变,那么这个几何体最多可以再添加 个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解高峰时段从总站乘16路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:
14,23,16,25,23,28,26,27,23,25.
(1)计算这10个班次乘车人数的平均数;
(2)如果16路车在高峰时段从总站共出车60个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com