
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
销售单价(元) | 40+x |
销售量y(件) |
|
销售玩具获得利润W(元) |
|
(2)在(1)问条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
【答案】(1)600﹣10x, ﹣10x2+500x+6000或(10+ x)(600﹣10x);(2)玩具销售单价为50元或80元时,可获得10000元销售利润; (2)商场销售该品牌玩具获得的最大利润为8640元.
【解析】
(1)根据销售单价每涨1元,就会少售出10件玩具,销售量为(600-10x)件,销售玩具获得利润为-10x2+500x+6000;
(2)根据获得利润为10000元,列方程求解;
(3)根据题意得方程组,求得4≤x≤6,根据二次函数的性质得到当4≤x≤6时,y随x增大而增大,于是得到结论.
解:(1)由题意得,销售量为:y=600-10x,
销售玩具获得利润为:W=(40+x-30)(600-10x)=-10x2+500x+6000;
故答案为:600-10x,-10x2+500x+6000;
(2)列方程得:﹣10x2+500x+6000=10000,
解得:x1=10,x2=40.
∴该玩具销售单价应定为50元或80元;
玩具销售单价为50元或80元时,可获得10000元销售利润;
(3)销售单价为在40元的基础上上涨x,
根据题意得![]() ,
,
解得:![]() ,
,
W=﹣10x2+500x+6000=﹣10(x﹣25)2+12250,
∵a=﹣10<0,对称轴x=25,
∴当![]() 时,y随x增大而增大,
时,y随x增大而增大,
∴当x=6时,W最大值=8640(元),
答:商场销售该品牌玩具获得的最大利润为8640元.


科目:初中数学 来源: 题型:
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
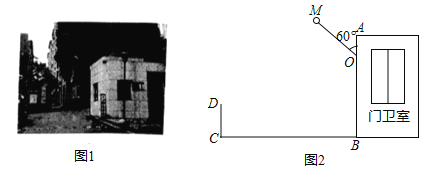
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是矩形
是矩形![]() 内的任意一点,连接
内的任意一点,连接![]() 、
、![]() 、
、![]() 、
、![]() , 得到
, 得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,
,![]() ,
,![]() ,
,![]() , 给出如下结论:①
, 给出如下结论:①![]() ②
②![]() ③若
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]() 点在矩形的对角线上.其中正确的结论的序号是( )
点在矩形的对角线上.其中正确的结论的序号是( )

A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为________.
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点坐标为M(1,0),直线y=x+m与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在y轴上.P(a,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
(1)求m的值及这个二次函数的解析式;
(2)若点P的横坐标为2,求△ODE的面积;
(3)当0<a<3时,求线段DE的最大值;
(4)若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
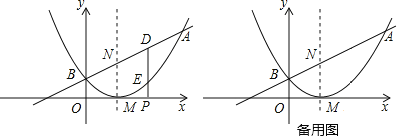
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
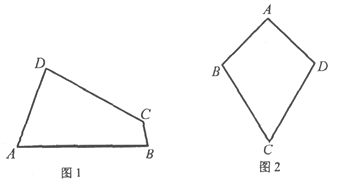
【题目】类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元.如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com