
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
先利用交点式求出抛物线解析式,则可对①进行判断;利用抛物线的对称性可对②进行判断;利用抛物线与x轴的交点坐标为(0,0),(4,0)可对③④进行判断;根据二次函数的性质求出x的值,即可对⑤进行判断.
设抛物线解析式为y=ax(x﹣4),
把(﹣1,5)代入得5=a×(﹣1)×(﹣1﹣4),解得:a=1,
∴抛物线解析式为y=x2﹣4x,所以①正确;
抛物线的对称轴为直线x=![]() =2,所以②正确;
=2,所以②正确;
∵抛物线与x轴的交点坐标为(0,0),(4,0),开口向上,
∴当0<x<4时,y<0,所以③错误;
抛物线与x轴的两个交点间的距离是4,所以④正确;
若A(x1,2),B(x2,3)是抛物线上两点,由x2﹣4x=2,解得:x1=![]() ,由x2﹣4x=3,解得:x2=
,由x2﹣4x=3,解得:x2=![]() ,若取x1=
,若取x1=![]() ,x2=
,x2=![]() ,则⑤错误.
,则⑤错误.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春临大地,学校决定给长12米,宽9米的一块长方形展示区进行种植改造现将其划分成如图两个区域:区域Ⅰ矩形ABCD部分和区域Ⅱ四周环形部分,其中区域Ⅰ用甲、乙、丙三种花卉种植,且EF平分BD,G,H分别为AB,CD中点.
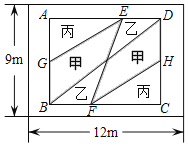
(1)若区域Ⅰ的面积为Sm2,种植均价为180元/m2,区域Ⅱ的草坪均价为40元/m2,且两区域的总价为16500元,求S的值.
(2)若AB:BC=4:5,区域Ⅱ左右两侧草坪环宽相等,均为上、下草坪环宽的2倍
①求AB,BC的长;
②若甲、丙单价和为360元/m2,乙、丙单价比为13:12,三种花卉单价均为20的整数倍.当矩形ABCD中花卉的种植总价为14520元时,求种植乙花卉的总价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
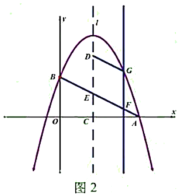
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 在第一象限的图象如图所示,过
在第一象限的图象如图所示,过![]() 上任意一点
上任意一点![]() ,作
,作![]() 轴垂线交
轴垂线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() 轴垂线,交
轴垂线,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() ,则
,则![]() __________.
__________.
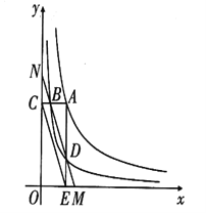
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
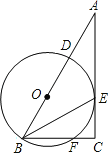
查看答案和解析>>
科目:初中数学 来源: 题型:
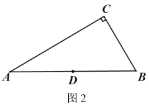
【题目】已知,在Rt△ABC和Rt△DEF中,∠ACB=∠EDF=90°,∠A=30°,∠E=45°,AB=EF=6,如图1,D是斜边AB的中点,将等腰Rt△DEF绕点D顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE,AC相交于点M,直线DF,BC相交于点N.
(1)如图1,当α=60°时,求证:DM=BN;
(2)在上述旋转过程中,![]() 的值是一个定值吗?请在图2中画出图形并加以证明;
的值是一个定值吗?请在图2中画出图形并加以证明;
(3)如图3,在上述旋转过程中,当点C落在斜边EF上时,求两个三角形重合部分四边形CMDN的面积.
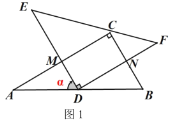
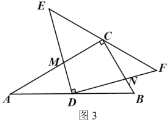
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com