
| A. | 10+5$\sqrt{2}$ | B. | 10+$\sqrt{2}$ | C. | 20+5$\sqrt{2}$ | D. | 10+10$\sqrt{2}$ |
科目:初中数学 来源: 题型:解答题
三角形 |  | 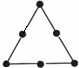 | 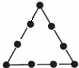 | … | 第n个 三角形 |
| 棋子个数 | 3 | 6 | 9 | … | P |
正方形 |  |  |  | … | 第n个 正方形 |
| 棋子个数 | 4 | 8 | 12 | … | Q |
正多边形 |  |  |  |  | 第n个 正多边形 |
| 棋子个数 | 3 | 8 | 15 | 24 | M |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图.
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,补充下列一个条件,不能使△ABD∽△ACB的是( )
如图,补充下列一个条件,不能使△ABD∽△ACB的是( )| A. | ∠1=∠C | B. | ∠2=∠ABC | C. | $\frac{AD}{AB}=\frac{AB}{AC}$ | D. | $\frac{AD}{AB}=\frac{AB}{BC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com