
 如图,补充下列一个条件,不能使△ABD∽△ACB的是( )
如图,补充下列一个条件,不能使△ABD∽△ACB的是( )| A. | ∠1=∠C | B. | ∠2=∠ABC | C. | $\frac{AD}{AB}=\frac{AB}{AC}$ | D. | $\frac{AD}{AB}=\frac{AB}{BC}$ |
分析 由图可知△ABC与△ABD中∠A为公共角,所以只要再找一组角相等,或一组对应边成比例即可满足△ABD∽△ACB;得出选项A、B、C满足△ABD∽△ACB,选项D不满足△ABD∽△ACB,即可得出结论.
解答 解:∵∠1=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴选项A不符合;
∵∠2=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴选项B不符合;
∵$\frac{AD}{AB}=\frac{AB}{AC}$,∠A=∠A,
∴△ABD∽△ACB,
∴选项C不符合;
虽然$\frac{AD}{AB}=\frac{AB}{BC}$,但∠A≠∠B,
∴△ABD与△ACB不相似,
∴选项D符合.
故选:D.
点评 本题考查了相似三角形的判定,此题主要考查学生对相似三角形判定定理的理解和掌握,难度不大,属于基础题,要求学生应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 10+5$\sqrt{2}$ | B. | 10+$\sqrt{2}$ | C. | 20+5$\sqrt{2}$ | D. | 10+10$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
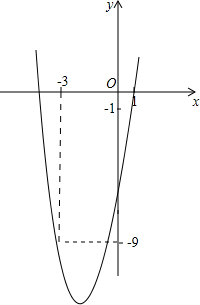 如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).
如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com