
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C,D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=![]() ,求EF的长.
,求EF的长.
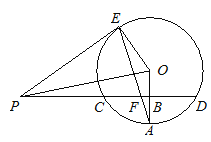
【答案】(1)CD的长为![]() ;
;
(2)证明见解析;
(3)EF的长为10.
【解析】试题分析:(1)首先连接OD,由直线PD垂直平分 O的半径OA于点B, O的半径为8,可求得OB的长,又由勾股定理,可求得BD的长,然后由垂径定理,求得CD的长;(2)由PE是 O的切线,易证得∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF;(3)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PFsinA=13×![]() =5,又由等腰三角形的性质,求得答案.
=5,又由等腰三角形的性质,求得答案.
试题解析:(1)连接OD,
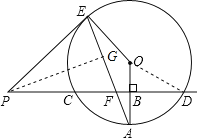
∵直线PD垂直平分O的半径OA于点B,O的半径为8,
∴OB=![]() OA=4,BC=BD=
OA=4,BC=BD=![]() CD,
CD,
∴在Rt△OBD中,BD=![]() ,
,
∴CD=2BD=![]() ;
;
(2)∵PE是O的切线,
∴∠PEO=90°,
∴∠PEF=90°∠AEO,∠PFE=∠AFB=90°∠A,
∵OE=OA,
∴∠A=∠AEO,
∴∠PEF=∠PFE,
∴PE=PF;
(3)过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°,
∵∠PFG=∠AFB,
∴∠FPG=∠A,
∴FG=PFsinA=13×![]() =5,
=5,
∵PE=PF,
∴EF=2FG=10.


科目:初中数学 来源: 题型:
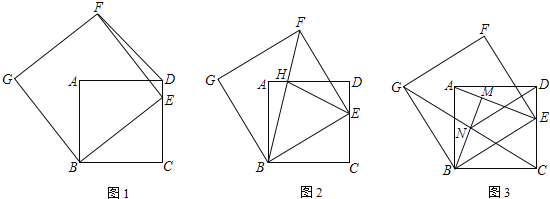
【题目】如图1,E为边长为1的正方形ABCD中CD边上的一动点(不含点C、D),以BE为边作图中所示的正方形BEFG
(1)求∠ADF的度数
(2)如图2,若BF交AD于点H,连接EH,求证:HB平分∠AHE
(3)如图3,连接AE、CG,作BM⊥AE于点M,BM交GC于点N,连接DN.当E在CD上运动时,求证:NC=NG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店把某种“大运”纪念品按成本价提高50%后标价,又以8折(即按标价的80%优惠售出,结果每件仍获利2.4元,则这种纪念品的成本是
A.3元B.4.8元C.6元D.12元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )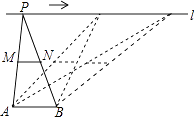
A.②③
B.②⑤
C.①③④
D.④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
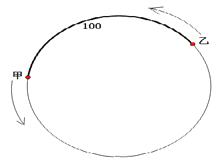
【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为![]() 米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为
米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为![]() 秒.
秒.
(1)若![]() =5,求甲、乙两人第1次相遇的时间;
=5,求甲、乙两人第1次相遇的时间;
(2)当![]() 时,甲、乙两人第1次相遇.
时,甲、乙两人第1次相遇.
①求![]() 的值;
的值;
②若![]() 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( ) 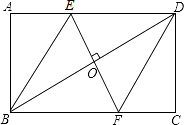
A.2 ![]()
B.3 ![]()
C.![]()
![]()
D.6 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com