
【题目】定义![]() 为一次函数
为一次函数![]() 的特征数.
的特征数.
(1)若特征数是![]() 的一次函数为正比例函数,求
的一次函数为正比例函数,求![]() 的值;
的值;
(2)设点![]() 分别为抛物线y=(3x+2m)(x-4)
分别为抛物线y=(3x+2m)(x-4)![]() 与
与![]() 轴的交点,其中
轴的交点,其中![]() ,且
,且![]() 的面积为4,
的面积为4,![]() 为原点,求图象过
为原点,求图象过![]() 两点的一次函数的特征数.
两点的一次函数的特征数.
【答案】(1)4;(2) (-12, -8![]() )或(2,-4).
)或(2,-4).
【解析】(1)由题中的新定义[p,q]为一次函数y=px+q的特征数,表示出特征数为[2k+2,3k-12]表示的一次函数,根据一次函数y=kx+b中b=0,列出关于k的方程,求出方程的解即可得到k的值;
(2)先分别求出抛物线与x轴、y轴的交点,然后根据![]() 的面积为4,得到关于m的方程,解方程求得m的值后,确定出A、B两点的坐标,即可求得图象过
的面积为4,得到关于m的方程,解方程求得m的值后,确定出A、B两点的坐标,即可求得图象过![]() 两点的一次函数的特征数.
两点的一次函数的特征数.
(1)根据题意得:特征数为[2k+2,3k-12]的一次函数是y=(2k+2)x+3k-12,
又此一次函数为正比例函数,
∴3k-12=0,解得:k=4;
(2) y=(3x+2m)(x-4)中,令y=0,则有(3x+2m)(x-4)=0,解得:x1=![]() ,x2=4,
,x2=4,
令x=0,则有y=-8m,
所以抛物线与x轴的交点为A1(![]() ,0),A2(4,0),
,0),A2(4,0),
与y轴的交点为B(0,-8m),
若![]() =4,则;4=
=4,则;4=![]() ,因为
,因为![]() ,所以m=
,所以m=![]() ,
,
若![]() =4,则;4=
=4,则;4=![]() ,因为
,因为![]() ,所以m=
,所以m=![]() ,
,
所以满足题设条件,抛物线的解析式为与坐标轴的交点为
A(![]() ,0),B(0,-4
,0),B(0,-4![]() )或A(4,0),B(0,-2),
)或A(4,0),B(0,-2),
利用待定系数法可求得直线AB的解析式为:
y=-12x-4![]() 或y=
或y=![]() x-2,
x-2,
图象过A,B 两点的一次函数的特征数为(-12, -4![]() )或(
)或(![]() ,-2).
,-2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
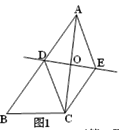
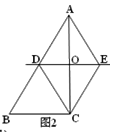
【题目】如图,已知△ABC,AC的垂直平分线交AB于点D,交AC于点O,过点C作CE∥AB交直线OD于点E,连接AE、CD.
⑴如图1,求证:四边形ADCE是菱形;
⑵如图2,当∠ACB=90°,BC=6,△ADC的周长为18时,求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠ACD是△ABC的一个外角,我们容易证明∠ACD=∠A+∠B,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
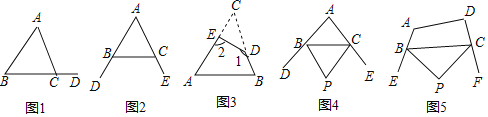
尝试探究:(1)如图2,∠DBC与∠ECB分别为△ABC的两个外角,则∠DBC+∠ECB ∠A+180°(横线上填>、<或=)
初步应用:(2)如图3,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=135°,则∠2-∠C= .
解决问题:(3)如图4,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
(4)如图5,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,请利用上面的结论探究∠P与∠A、∠D的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有( )
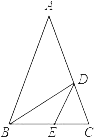
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.
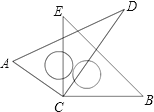
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的暖瓶和水杯的售价信息,回答下列问题:
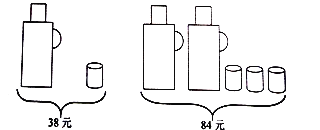
(1)一个暖瓶与一个水杯的售价分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,在新年期间,两家商场都在搞促销活动.甲商场规定:这两种商品都打8.5折;乙商场规定:两种商品都不打折,但买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和16个水杯,请问这个单位选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三条长度均为a的线段,分别按以下要求画圆.
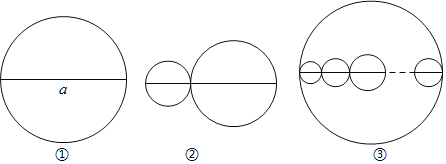
(1)如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2,请指出C1和C2的数量关系,并说明理由;
(2)如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若千小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为 .(直接填写答案,结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如下规律摆放三角形:
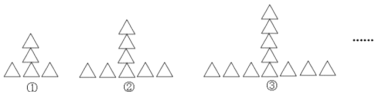
(1)图④中分别有多少个三角形?
(2)按上述规律排列下去,第n个图形中有多少个三角形?
(3)按上述规律排列下去,第2014个图形中有多少个三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com