
【题目】如图,已知△ABC,AC的垂直平分线交AB于点D,交AC于点O,过点C作CE∥AB交直线OD于点E,连接AE、CD.
⑴如图1,求证:四边形ADCE是菱形;
⑵如图2,当∠ACB=90°,BC=6,△ADC的周长为18时,求AC的长度.
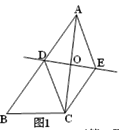
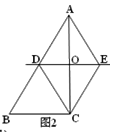
【答案】(1)见解析;(2)AC=8
【解析】(1)利用直线DE是线段AC的垂直平分线,得出AC⊥DE,即∠AOD=∠COE=90°,进而得出△AOD≌△COE,即可得出四边形ADCE是菱形;
(2)利用当∠ACB=90°时,OD∥BC,即有△ADO∽△ABC,即可得出AC的长.
详(1)证明:∴直线DE是线段AC的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°;
且AD=CD、AO=CO,
又∵CE∥AB,
∴∠1=∠2,
在△AOD和△COE中
 ,
,
∴△AOD≌△COE(AAS),
∴OD=OE,
∵A0=CO,DO=EO,
∴四边形ADCE是平行四边形,
又∵AC⊥DE,
∴四边形ADCE是菱形;
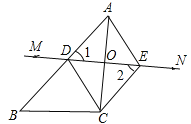
(2)当∠ACB=90°时,OD∥BC,
即有△ADO∽△ABC,
∴![]() ,
,
又∵BC=6,
∴OD=3,
又∵△ADC的周长为18,
∴AD+AO=9,
即AD=9-AO,
∴OD=![]() =3,
=3,
可得AO=4,
∴AC=8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
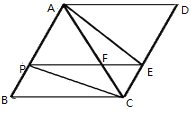
【题目】如图,在四边形ABCD中,![]() ,
,![]() ,连接AC,点P、E分别在AB、CD上,连接PE,PE与AC交于点F,连接PC,
,连接AC,点P、E分别在AB、CD上,连接PE,PE与AC交于点F,连接PC,![]()
![]() ,
,![]() .
.
(1)判断四边形PBCE的形状,并说明理由;
(2)求证:![]() ;
;
(3)当P为AB的中点时,四边形APCE是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
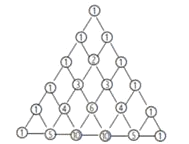
【题目】我国古代数学领域有些研究成果曾位居世界前列,其中“杨辉三角”就是一例.南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图中的三角形解释二项和的乘方规律.杨辉三角两腰上的数都是1,其余每个数都为它的上方(左右)两数之和,这个三角形给出了(a+b)n(n=1,2,3,4,5)的展开式(按a的次数由大到小的顺序)的系数规律.例如,此三角形中第3行的3个数1,2,1,恰好对应着(a+b)2=a2+2ab+b2展开式中各项的系数:第4行的4个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中各项的系数,等等.利用上面呈现的规律填空:(a+b)6=a6+6a5b+________+20a3b3+15a2b4+ ________+b6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a1,第二个数记为a2,…,第n个数记为an.
(1)请写出29后面的第一个数;
(2)通过计算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根据你发现的规律求a100的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,七(1)班的小明等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话,试根据对话中的信息,解答下列问题:
儿子:爸爸,成人门票是每张20元;学生门票是五折优惠;
团体票(16人及16人以上),按成人票的六折优惠.
爸爸:我们成人、学生一共12人,共需200元.
(1)设小明他们一共去了学生![]() 人,则成人购买门票的总费用为: 元;(用含
人,则成人购买门票的总费用为: 元;(用含![]() 的代数式表示)
的代数式表示)
(2)七(1)班小明他们一共去了几个成人、几个学生?
(3)正在购票时,小明发现七(2)班的小军等10名同学和他们的7名家长共17人也来购票,他们准备联合一起购买门票,请你为这29人的团队设计出最省的购票方案(直接写出方案即可,无需讨论),并求出此时的购票费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某学校决定开设民族器乐选修课.为了更贴合学生的兴趣,对学生最喜爱的一种民族乐器进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
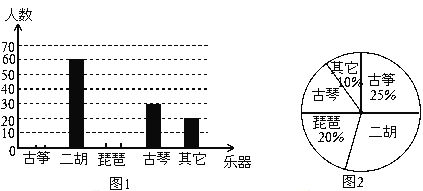
(1)在这次抽样调查中,共调查 名学生;
(2)请把条形图(图1)补充完整;
(3)求扇形统计图(图2)中,二胡部分所对应的圆心角的度数;
(4)如果该校共有学生1500名,请你估计最喜爱古琴的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 为一次函数
为一次函数![]() 的特征数.
的特征数.
(1)若特征数是![]() 的一次函数为正比例函数,求
的一次函数为正比例函数,求![]() 的值;
的值;
(2)设点![]() 分别为抛物线y=(3x+2m)(x-4)
分别为抛物线y=(3x+2m)(x-4)![]() 与
与![]() 轴的交点,其中
轴的交点,其中![]() ,且
,且![]() 的面积为4,
的面积为4,![]() 为原点,求图象过
为原点,求图象过![]() 两点的一次函数的特征数.
两点的一次函数的特征数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com