
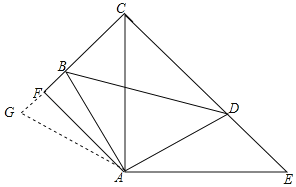
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF于点F.
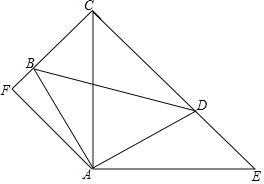
(1)求证:△ABC≌△ADE;
(2)已知BF的长为2,DE的长为6,求CD的长.
【答案】(1)见解析;(2)10
【解析】
(1)由∠BAD=∠CAE=90°得出∠BAC=∠DAE,即可得出△BAC≌△DAE(SAS);
(2)由(1)可知∠BCA=∠E=45°,∠CBA=∠EDA,CB=ED,延长BF到G,使得FG=FB,连接AG,证明△AFB≌△AFG(SAS),得出AB=AG=AD,∠ABF=∠G=∠CDA,证明△CGA≌△CDA(AAS),得出CD=CG,进而得出答案.
(1)证明:∵∠BAD=∠CAE=90°
∴∠BAC=90°﹣∠CAD,∠DAE=90°∠CAD,即∠BAC=∠DAE
在△BAC和△DAE中,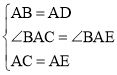 ,
,
∴△BAC≌△DAE(SAS);
(2)解:∵∠CAE=90°,AE=AC,
∴∠E=45°,
由(1)可知:△ABC≌△ADE,
∴∠BCA=∠E=45°,∠CBA=∠EDA,CB=ED,
延长BF到G,使得FG=FB,连接AG,如图所示:
∵AF⊥CF,
∴∠AFG=∠AFB=90°,
在△AFB和△AFG中,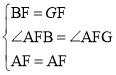 ,
,
∴△AFB≌△AFG(SAS),
∴AB=AG=AD,∠ABF=∠G=∠CDA
在△CGA和△CDA中,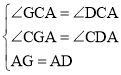 ,
,
∴△CGA≌△CDA(AAS),
∴CD=CG
∴CD=CB+BF+FG=CB+2BF=DE+2BF=6+2×2=10.


科目:初中数学 来源: 题型:
【题目】任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1),Q (x2,y2)的对称中心的坐标为![]() ,如图.
,如图.
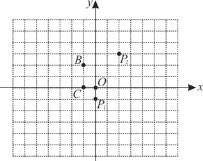
(1)在平面直角坐标系中,若点P1(0,-1),P2(2,3)的对称中心是点A,则点A的坐标为________;
(2)另取两点![]() ,
,![]() .有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点
.有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(a2b﹣2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=1,b=﹣2.
(2)先化简(1+![]() )÷
)÷![]() ,再从﹣1,0,1,2,3中选取一个合适的数作为x的值代入求值.
,再从﹣1,0,1,2,3中选取一个合适的数作为x的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
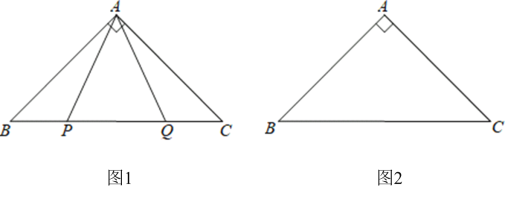
【题目】已知:在![]() 中,
中,![]() .
.
(1)如图1,![]() 是
是![]() 边上两点,
边上两点,![]() , 求
, 求![]() 的度数.
的度数.
(2)点![]() 是
是![]() 边上两动点(不与
边上两动点(不与![]() 重合), 点
重合), 点![]() 在点
在点![]() 左侧,且
左侧,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①依题意将图2补全.
②小明通过观察和实验,提出猜想:在点![]() 运动的过程中,始终有
运动的过程中,始终有![]() 为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明
为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明![]() 为等腰直角三角形,只需证
为等腰直角三角形,只需证![]() .
.
请参考上面的思路,帮助小明证明△APM 为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
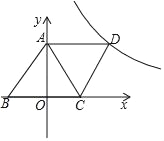
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=![]() (k为常数,k≠0,x>0)的图象经过点D.
(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=_____.
(2)已知在y=![]() 的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一斜坡坡顶![]() 处的同一水平线上有一古塔,为测量塔高
处的同一水平线上有一古塔,为测量塔高![]() ,数学老师带领同学在坡脚
,数学老师带领同学在坡脚![]() 处测得斜坡的坡角为
处测得斜坡的坡角为![]() ,且
,且![]() ,塔顶
,塔顶![]() 处的仰角为
处的仰角为![]() ,他们沿着斜坡攀行了
,他们沿着斜坡攀行了![]() 米,到达坡顶
米,到达坡顶![]() 处,在
处,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .
.
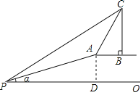
(1)求斜坡的高度![]() ;
;
(2)求塔高![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
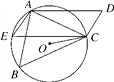
【题目】如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
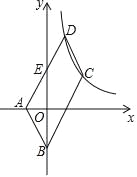
【题目】如图,平行四边形ABCD中,A(-1,0)、B(0,-2),顶点C、D在双曲线![]() (x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
(x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com