
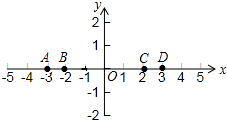 如图所示,C,D两点的横坐标分别为2,3.线段CD=1;B,D两点的横坐标分别为-2,3.线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1,请探究:
如图所示,C,D两点的横坐标分别为2,3.线段CD=1;B,D两点的横坐标分别为-2,3.线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1,请探究:分析 (1)根据题意,由点M(x1,O),N(x2,O),可以得到线段MN的长;
(2)根据题意,由点P(O,y1),Q(O,y2),可得线段PQ的长;
(3)由(1)和(2)及点P(x1,y1),Q(x2,y2),可得线段PQ的长.
解答 解:(1)∵点M(x1,O),N(x2,O),
∴线段MN的长为:|x1-x2|.
(2)∵点P(O,y1),Q(O,y2),
∴线段PQ的长为:|y1-y2|.
(3)∵点P(x1,y1),Q(x2,y2),
∴由(1)和(2)可得,线段PQ的长为:PQ=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.
点评 本题考查坐标与图形的性质,解题的关键是明确线段的长都为正值,用坐标表示就需要加上绝对值符号.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:初中数学 来源: 题型:解答题
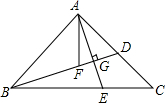 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
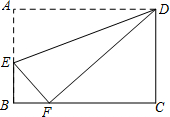 如图,长方形ABCD中,点E 在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=5,DC=3,则BF的长是( )
如图,长方形ABCD中,点E 在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=5,DC=3,则BF的长是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:单选题
瑞安某服装店十月份的营业额为8000元,改进经营措施后营业额稳步上升,十二月份的营业额达到11520元.如果平均每月的增长率为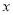 ,则由题意可列出方程为( )
,则由题意可列出方程为( )
A. 8000×2x=11520 B. 8000(1+x)=11520
C. 8000(1+2x)=11520 D. 8000(1+x)2=11520
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
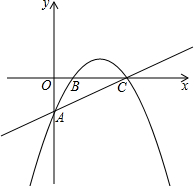 如图:在平面直角坐标系中,直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A,抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,交x轴于另外一点B.
如图:在平面直角坐标系中,直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A,抛物线y=-$\frac{1}{2}$x2+bx+c经过A、C两点,交x轴于另外一点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com