
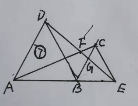
【题目】如图![]() 绕点B顺时针旋转60°得到
绕点B顺时针旋转60°得到![]() ,A、B、E三点共线,AC交DE于F,BC交DE于G,下列结论不正确的是( )
,A、B、E三点共线,AC交DE于F,BC交DE于G,下列结论不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据旋转的性质得出![]()
![]() ,推出AB=BD,∠ABD=60°,则可证明
,推出AB=BD,∠ABD=60°,则可证明![]() 为等边三角形,则
为等边三角形,则![]() ,根据CB=BE,∠CBE=60°,则可证明
,根据CB=BE,∠CBE=60°,则可证明![]() 为等边三角形,则∠DBC=60°,则∠AFD=180°-∠DAF-(∠ADB+∠BDE)=60°,即可证明
为等边三角形,则∠DBC=60°,则∠AFD=180°-∠DAF-(∠ADB+∠BDE)=60°,即可证明![]() ,根据∠ABD=60°,∠CBE=60°,即可证明
,根据∠ABD=60°,∠CBE=60°,即可证明![]() .
.
解:根据旋转的性质得出![]()
![]() ,
,
∴AB=BD,∠ABD=60°,∠BAC=∠BDE
∴![]() 为等边三角形
为等边三角形
∴![]() ,故A正确;
,故A正确;
∵CB=BE,∠CBE=60°
∴![]() 为等边三角形
为等边三角形
∴∠DBC=60°,
∴∠AFD=180°-∠DAF-(∠ADB+∠BDE)=180°- ∠ADB -(∠DAF +∠BDE)=180°-∠ADB -(∠DAF +∠BAC)= ∠ABD =60°,
∴![]() ,故B正确;
,故B正确;
∵∠ABD=60°,∠CBE=60°
∴![]() ,故C正确;
,故C正确;
D无法确定,故错误.
故选D.


科目:初中数学 来源: 题型:
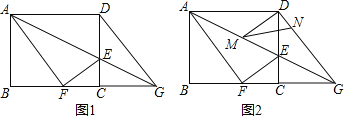
【题目】如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.
(1)求线段CE的长;
(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.
①写出y关于x的函数解析式,并求出y的最小值;
②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、D在⊙O上,连结BC,过D作PF∥AC交AB于E,交⊙O于F,交BC于点G,交过B点的直线于点P,且∠BPF=∠ADC.
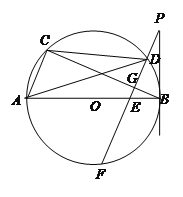
(1)判断直线BP与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为![]() ,AC=2,BE=1,求BP的长.
,AC=2,BE=1,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的 反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是 “兵”面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的机会大小,某 实验小组做了棋子下掷实验,实验数据如下表:
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“兵”字面朝上频数 | 14 | 38 | 47 | 52 | 66 | 78 | 88 | |
“兵”字面朝上频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.56 | 0.55 |
(1)请将数据表补充完整:
(2)在图中画出“兵”字面朝上的频率分布折线图:
(3)如果实验继续进行下去,根据上表的数据,这个实验所得频率将逐渐稳定到某 一个数值附近,请你估计该随机事件在每次实验时发生的机会大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
如图1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延长CA到点F,使得AF=AC,连接DF、BE,则线段BE与DF的数量关系为 ,位置关系为 ;
(2)(拓展研究)
将△ADE绕点A旋转,(1)中的结论有无变化?仅就图(2)的情形给出证明;
(3)(解决问题)
当AB=2,AD=![]() ,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.
,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com