练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     从2，3，4，5中任意选两个数，记作和，那么点(，)在函数图象上的概率是     (     )

    A．        B．         C．     D．       


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若实数x,y适合不等式xy>1,x+y≥-2,则(　　)

    (A)x>0,y>0  (B)x<0,y<0

    (C)x>0,y<0  (D)x<0,y>0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列各点中，在函数的图象上的是（    ）

    A．（2，1）       B．（－2，1）   C．（2，－2）        D．（1，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


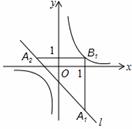
    如图，在平面直角坐标系xOy中，已知直线l：y=﹣x﹣1，双曲线y=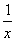，在l上取一点A1，过A1作x轴的垂线交双曲线与点B1，过B1作y轴的垂线交l于点A2，请继续操作并探究；过A2作x轴的垂线交双曲线于点B2，过B2作y轴的垂线交l于点A3，…，这样依次得到l上的点A1，A2，A3，…，An，…记点An的横坐标为an，若a1=2，则a2015=       ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


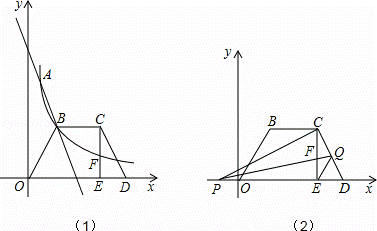
    如图（1），直线y=k1 x+b与反比例函数y=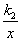的图象交于点A（1，6），B（a，3）两点．

    （1）求k1、k2的值；

    （2）如图（1），等腰梯形OBCD中，BC∥OD，OB=CD，OD边在x轴上，过点C作CE⊥OD于点E，CE和反比例函数的图象交于点F，当梯形OBCD的面积为12时，请判断FC和EF的大小，并说明理由；

    （3）如图（2），已知点Q是CD的中点，在第（2）问的条件下，点P在x轴上，从原点O出发，沿x轴负方向运动，设四边形PCQE的面积为S1，△DEQ的面积为S2，当∠PCD=90°时，求P点坐标及S1：S2的值．


    查看答案和解析>>

    科目：初中数学 来源： 题型：


     二次函数y=kx- 6x + 3的图像与X轴有交点，则K的取值范围是（     ）

    A.K﹤3      B.K﹤3且K≠0       C.K≤3       D.K≤3且K≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，反比例函数y= (x＜0)的图象经过点P ，则k的值为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


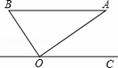
    如图，在Rt△ABO中，斜边AB=1．若OC∥BA，∠AOC=36°，则（　　）

    　    A． 点B到AO的距离为sin54°

    　    B．  点B到AO的距离为tan36°

    　    C． 点A到OC的距离为sin36°sin54°

    　    D． 点A到OC的距离为cos36°sin54°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


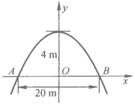
    .有一座抛物线型拱桥(如图所示)，正常水位时桥下河面宽20 m，河面距拱顶4 m. 试求：

    (1)在如图26－10所示的平面直角坐标系中，求出抛物线解析式；

    (2)为了保证过往船只顺利航行，桥下水面的宽度不得小于18m，求水面在正常水位基础上涨多少米时，就会影响过往船只?

    查看答案和解析>>

    同步练习册答案