
【题目】皮皮拿着一块正方形纸板在阳光下做投影实验,正方形纸板在投影面上形成的投影不可能是( )
A.正方形
B.长方形
C.线段
D.梯形
科目:初中数学 来源: 题型:
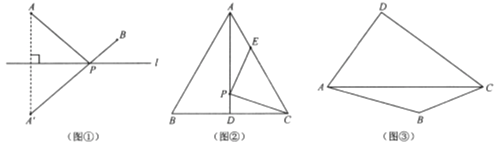
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为0,点A、B、C是数轴上的三点,点B对应的数位1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
(1)求点A、C分别对应的数;
(2)求点P、Q分别对应的数(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若四边形AEDF的周长为24,AB=15,求AC的长;
(2)求证:EF垂直平分AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年宁波市中考新增英语口语听力自动化考试,考试需要耳麦,已知甲耳麦比乙耳麦贵20元,某校购买了甲耳麦40个、乙耳麦60个,共花费了6000元,假设甲耳麦每个x元,由题意得( )
A. 40x+60(x–20)=6000 B. 40x+60(x+20)=6000
C. 60x+40(x–20)=6000 D. 60x+40(x+20)=6000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com