
(本 题14分)已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线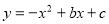 经过坐标原点O和x轴上另一点E(4,0)。
经过坐标原点O和x轴上另一点E(4,0)。
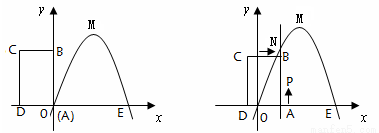
(1)当x取何值时,该抛物线的最大值是多少?
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示)。
① 当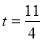 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
② 以P、N、C、D为顶点的多边形面积是否可能为5,若有可能,求出此时N点的坐标;若无可能,请说明理由.
(1)当x=2时,该抛物线的最大值是4;(2)①点P不在直线ME上,理由详见解析;②以P、N、C、D为顶点的多边形面积可能为5,当t=1时,此时N点的坐标(1,3);当t=2时,此时N点的坐标(2,4)理由详见解析
【解析】
试题分析:(1)因抛物线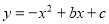 经过坐标原点O(0,0)和点E(4,0)
经过坐标原点O(0,0)和点E(4,0)
故可得c=0,b=4
所以抛物线的解析式为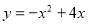
得当x=2时,该抛物线的最大值是4.
(2)① 点P不在直线ME上.
已知M点的坐标为(2,4),E点的坐标为(4,0),
设直线ME的关系式为y=kx+b.
于是得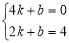 ,解得
,解得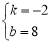
所以直线ME的关系式为y=-2x+8.
由已知条件易得,当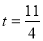 时,OA=AP=
时,OA=AP=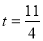 ,
,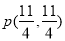
∵ P点的坐标不满足直线ME的关系式y=-2x+8.
∴ 当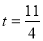 时,点P不在直线ME上.
时,点P不在直线ME上.
②以P、N、C、D为顶点的多边形面积可能为5
∵ 点A在x轴的非负半轴上,且N在抛物线上,
∴ OA=AP=t.
∴ 点P,N的坐标分别为(t,t)、(t,-t2+4t)
∴ AN=-t2+4t (0≤t≤3),
∴ AN-AP=(-t2+4t)-t=-t 2+3t=t(3-t)≥0 ,
∴ PN=-t2+3t 2分
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,∴ S=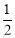 DC·AD=
DC·AD=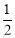 ×3×2=3.
×3×2=3.
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形
∵ PN∥CD,AD⊥CD,
∴ S=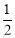 (CD+PN)·AD=
(CD+PN)·AD=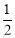 [3+(-t2+3t)]×2=-t2+3t+3
[3+(-t2+3t)]×2=-t2+3t+3
当-t2+3t+3=5时,解得t=1、2
而1、2都在0≤t≤3范围内,故以P、N、C、D为顶点的多边形面积为5
综上所述,当t=1、2时,以点P,N,C,D为顶点的多边形面积为5,
当t=1时,此时N点的坐标(1,3)
当t=2时,此时N点的坐标(2,4)
考点:二次函数的综合运用


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源:2014-2015学年河北省廊坊市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转 度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=
度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF= ,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE。其中正确的是________(写出正确结论的序号)。
,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE。其中正确的是________(写出正确结论的序号)。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级上学期期中考试数学试卷(解析版) 题型:选择题
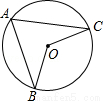
如右图所示,点A,B,C在圆O上,∠A=64°,则∠BOC的度数是( )
A.26° B.116° C.128° D.154°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级10月月考数学试卷(解析版) 题型:解答题
(本题8分)直线y=2x+2与x轴、y轴分别交于A、B两点,将△AOB绕点O顺时针旋转900,得到△A1OB1 。
(1)在图中画出△A1OB1;
(2)求经过A,A1,B1三点的抛物线的解析式。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级10月月考数学试卷(解析版) 题型:填空题
已知二次函数的图象开口向下,且经过原点。请写出一个符合条件的二次函数的解析式:________21。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:选择题
圆心距为6的两圆相外切,则以这两个圆的半径为根的一元二次方程是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com