
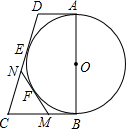
 如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )| A、9 | ||
| B、10 | ||
C、3
| ||
D、2
|
| 9 |
| 2 |
| 9 |
| 2 |
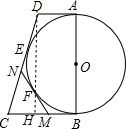 解:作DH⊥BC于H,如图,
解:作DH⊥BC于H,如图,| 9 |
| 2 |
| 9 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
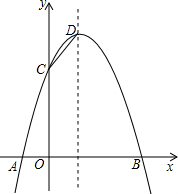 如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:
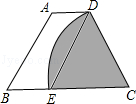 如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )
如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )| A、2π | B、4π | C、6π | D、12π |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角△ABC中,∠ACB=90°,点D、E在AB上,且∠DCE=45°,BE=2,AD=3.
如图,等腰直角△ABC中,∠ACB=90°,点D、E在AB上,且∠DCE=45°,BE=2,AD=3.查看答案和解析>>
科目:初中数学 来源: 题型:
 为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为
为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为查看答案和解析>>
科目:初中数学 来源: 题型:
| A、打开电视,正在直播NBA篮球赛 |
| B、早晨太阳一定从东方升起 |
| C、掷两次硬币,一定有一次正面朝上 |
| D、365人中一定有两人同一天出生 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com