Question

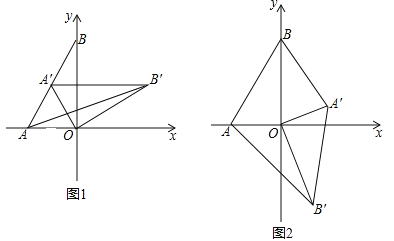
【题目】如图1，在平面直角坐标系，O为坐标原点，点A（﹣1，0），点B（0，）．

（1）求∠BAO的度数；

（2）如图1，将△AOB绕点O顺时针得△A′OB′，当A′恰好落在AB边上时，设△AB′O的面积为S1，△BA′O的面积为S2，S1与S2有何关系？为什么？

（3）若将△AOB绕点O顺时针旋转到如图2所示的位置，S1与S2的关系发生变化了吗？证明你的判断．

Answer 1

【答案】(1) ∠BAO=60°；(2) S1=S2;(3) S1=S2不发生变化；理由见解析.

【解析】

试题分析：（1）先求出OA，OB，再利用锐角三角函数即可得出结论；

（2）根据等边三角形的性质可得AO=AA＇，再根据直角三角形30°角所对的直角边等斜边的一半求出AO=AB，然后求出AO=AA’，，然后再根据等边三角形的性质求出点O到AB的距离等于点A＇到AO的距离，然后根据等底等高的三角形的面积相等解答；

（3）根据旋转的性质可得BO=OB＇，AA＇=OA＇，再求出∠AON=∠A＇OM，然后再证明ΔAON≌ΔA＇OM，可得AN=A＇M，然后利用等底等高的三角形面积相等证明.

试题解析：（1）∵A（﹣1，0），B（0， ），

∴OA=1，OB=，

在Rt△AOB中，tan∠BAO==，

∴∠BAO=60°；

（2）∵∠BAO=60°，∠AOB=90°，

∴∠ABO=30°，

∴CA'=AC=AB，

∴OA'=AA'=AO，

根据等边三角形的性质可得，△AOA'的边AO、AA'上的高相等，

∴△BA'O的面积和△AB'O的面积相等（等底等高的三角形的面积相等），

即S1=S2.

（3）S1=S2不发生变化；

理由：如图，过点'作A'M⊥OB．过点A作AN⊥OB'交B'O的延长线于N，

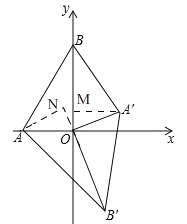
∵△A'B'O是由△ABO绕点O旋转得到，

∴BO=OB'，AO=OA'，

∵∠AON+∠BON=90°，∠A'OM+∠BON=180°﹣90°=90°，

∴∠AON=∠A'OM，

在△AON和△A'OM中，

，

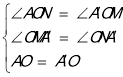∴△AON≌△A'OM（AAS），

∴AN=A'M，

∴△BOA'的面积和△AB'O的面积相等（等底等高的三角形的面积相等），

即S1=S2．