
【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,
求证: ![]()
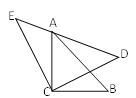
【答案】证明见解析.
【解析】试题分析:连结BD,根据等边三角形的性质就可以得出△AEC≌△BDC,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出结论.
试题解析:证明:连结BD,
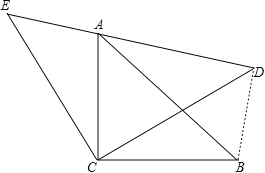
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
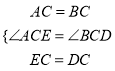 ,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
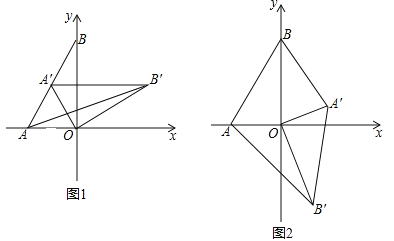
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,![]() ).
).
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
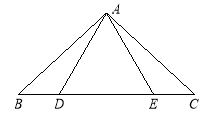
【题目】如图,点D,E在△ABC的边BC上,连 接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②③:①③②;②③①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B(3,﹣2)在平面直角坐标系中,按要求完成下列个小题.
(1)写出与点A关于y轴对称的点C的坐标,并在图中描出点C;
(2)在(1)的基础上,点B,C表示的是两个村庄,直线a表示河流,现要在河流a上的某点M处修建一个水泵站,向B、C两个村庄供水,并且使得管道BM+CM的长度最短,请你在图中画出水泵站M的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com