
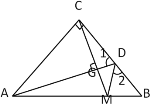
【题目】△ABC中,AC=BC,∠ACB=90°,CD=BD,∠1=∠2,求证:CM⊥AD。
【答案】见解析.
【解析】
过点C作CE⊥AB交AB于点E,交AD于点F,AD与CM交于点G,根据∠B=∠BCE=45°,CD=BD,∠1=∠2证明△CDF≌△BDM,得到CF=BM,然后再由AC=BC及![]() 通过SAS证明△ACF≌△CBM,得到∠CAF=∠BCM,再根据角之间的等量代换可证明∠CFG+∠ECM=90°,问题得证.
通过SAS证明△ACF≌△CBM,得到∠CAF=∠BCM,再根据角之间的等量代换可证明∠CFG+∠ECM=90°,问题得证.
证明:过点C作CE⊥AB交AB于点E,交AD于点F,AD与CM交于点G,
∵AC=BC,∠ACB=90°,
∴∠B=∠BCE=45°,
在△CDF和△BDM中,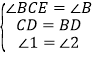 ,
,
∴△CDF≌△BDM(ASA),
∴CF=BM,
在△ACF和△CBM中, ,
,
∴△ACF≌△CBM(SAS),
∴∠CAF=∠BCM,
∵∠BCM +∠ECM =∠CAF+∠EAF=45°,
∴∠ECM =∠EAF,
∵∠AFE=∠CFG,且∠AFE+∠EAF=90°,
∴∠CFG+∠ECM=90°,即∠CGF=90°,
∴CM⊥AD.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以![]() cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.
阅读下列材料:
问题:利用一元一次方程将0.![]() 化成分数.
化成分数.
解:设0.![]() =x.
=x.
方程两边都乘以10,可得10×0.![]() =10x
=10x
由0.![]() =0.777…,可知10×0.
=0.777…,可知10×0. ![]() =7.777…=7+0.
=7.777…=7+0.![]()
即7+x=10x.(请你体会将方程两边都乘以10起到的作用)
可解得x=![]() ,即0.
,即0.![]() =
=![]() .
.
(1)填空:将0.![]() 写成分数形式为 .
写成分数形式为 .
(2)请你仿照上述方法把下列两个小数化成分数,要求写出利用一元一次方程进行解答的过程:①0.![]() ,②0.43
,②0.43![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
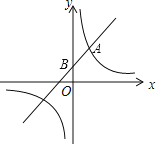
【题目】如图,一次函数y=kx+b(k≠0)经过点B(0,1),且与反比例函数y=![]() (m≠0)的图象在第一象限有公共点A(1,2).
(m≠0)的图象在第一象限有公共点A(1,2).
(1)求一次函数与反比例函数的解析式;
(2)根据图象写出当x取何值时,一次函数的值小于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别是 6,﹣8,M、N、P为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度为M点的3倍,点P从原点出发速度为每秒1个单位.
(1)若点M向右运动,同时点N向左运动,求多长时间点M与点N相距54个单位?
(2)若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“元旦”期间,平价商场对该商场商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
小于等于 400 元 | 不优惠 |
超过 400 元,但不超过 600元 | 按售价打九折 |
超过 600 元 | 其中 600 元部分八折优惠,超过 600 元的部分打六折优惠 |
按上述优惠条件,若小华一次性购买售价为 80 元/件的商品 n 件时,实际付款 504 元, 则 n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地之间的距离为20千米,甲步行,乙骑车,两人沿着相同路线,由A地到B地匀速前行,甲、乙行进的路程s与x(小时)的函数图象如图所示.(1)乙比甲晚出发___小时;(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,x的取值范围是___.
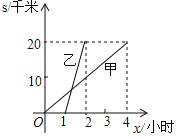
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
(1)本次调查共调查了 人,“比较了解”所占扇形统计图圆心角的度数为 ;
(2)请将两个统计图补充完整;
(3)若玲玲所在的学校有![]() 人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
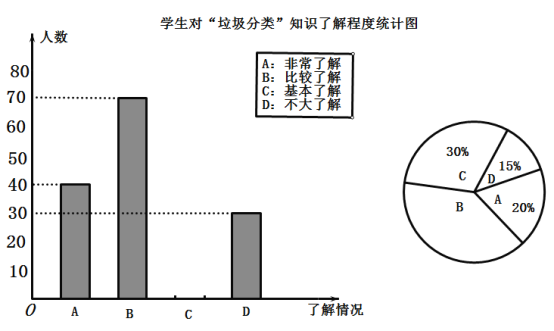
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com