
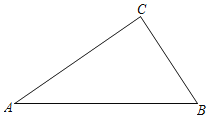
【题目】如图,在Rt△ABC中,∠ACB=90°,两直角边AC=8cm,BC=6cm.
(1)作∠BAC的平分线AD交BC于点D;(尺规作图,不写作法,保留作图痕迹)
(2)计算△ABD的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用尺规作出∠CAB的角平分线即可;
(2)作DE⊥AB,垂足为E.设CD=DE=x,在Rt△DEB中,利用勾股定理构建方程即可解决问题.
解:(1)作图如下:
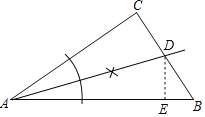
AD是∠ABC的平分线.
(2)在Rt△ABC中,由勾股定理得:
AB=![]() =
=![]() =10,
=10,
作DE⊥AB,垂足为E.
∵∠ACB=90°,AD是∠ABC的平分线,
∴CD=DE,
设CD=DE=x,
∴DB=6﹣x,
∵∠C=∠AED=90°,AD=AD,DC=DE,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE=8,
∴EB=AB﹣AE=10﹣8=2,
在Rt△DBE中由勾股定理得:x2+22=(6﹣x)2
解方程得x=![]() ,
,
∴S=![]() ABDE
ABDE![]() =
=![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
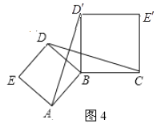
【题目】(解决问题)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正三角形
为边,分别作正三角形![]() 和正三角形
和正三角形![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,当点![]() ,
,![]() ,
,![]() 在同一直线上时,线段
在同一直线上时,线段![]() 与
与![]() 的大小关系是__________;
的大小关系是__________;
(2)如图2,当![]() ,
,![]() ,
,![]() 为三角形的顶点时(点
为三角形的顶点时(点![]() ,
,![]() ,
,![]() 不在同一条直线上),判断线段
不在同一条直线上),判断线段![]() 与
与![]() 的大小关系是否发生改变,并说明理由;
的大小关系是否发生改变,并说明理由;
(类比猜想)
(3)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正方形,连接
为边,分别作正方形,连接![]() ,
,![]() ,如图3和图4所示.判断线段
,如图3和图4所示.判断线段![]() 与
与![]() 的大小关系,并在图4(点
的大小关系,并在图4(点![]() ,
,![]() ,
,![]() 不在同一条直线上)中证明你的判断;
不在同一条直线上)中证明你的判断;
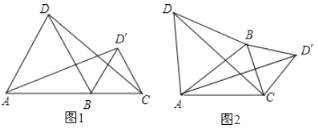
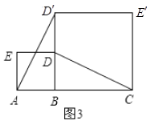
(推广应用)(4)上面的这些结论能否推广到任意正多边形(不必证明)?
(5)如图5,![]() 与
与![]() 的大小关系是__________,并写出它们分别在哪两个全等三角形中;
的大小关系是__________,并写出它们分别在哪两个全等三角形中;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
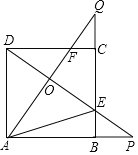
【题目】如图,正方形ABCD的边长是![]() ,连接
,连接![]() 交于点O,并分别与边
交于点O,并分别与边![]() 交于点
交于点![]() ,连接AE,下列结论:
,连接AE,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 当
当![]() 时,
时, ![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
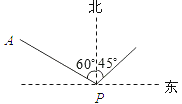
【题目】如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正东方向.求货船的航行速度.(精确到0.1海里/时,参考数据:![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移到△DCE,连接AD,BD,下列结论错误的是( )
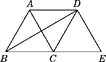
A.AD=BCB.BD⊥DE
C.四边形ACED是菱形D.四边形ABCD的面积为4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
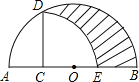
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
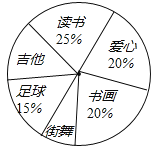
(1)该班的学生共有 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() (0,
(0, ![]() )
)![]() .
.
(1)求抛物线的解析式.
(2)抛物线与![]() 轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
(3)在(2)的前提下,过点B的直线![]() 与
与![]() 轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与
轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与![]() 相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
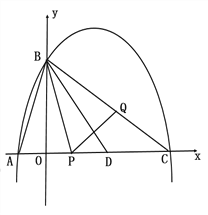
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com