
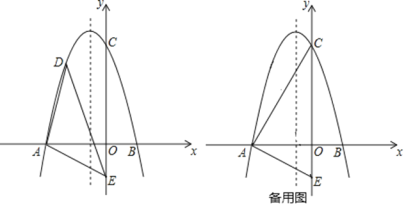
【题目】如图所示,在平面直角坐标系中,二次函数![]() 交x轴于
交x轴于![]() ,
,![]() ,在y轴上有一点
,在y轴上有一点![]() ,连接AE.
,连接AE.
![]() 求二次函数的表达式;
求二次函数的表达式;
![]() 点D是第二象限内的抛物线上一动点.
点D是第二象限内的抛物线上一动点.
①求![]() 面积最大值并写出此时点D的坐标;
面积最大值并写出此时点D的坐标;
②若![]() ,求此时点D坐标;
,求此时点D坐标;
【答案】(1)![]() ;(2)①D(
;(2)①D(![]() ,
,![]() );
);![]() ;②
;②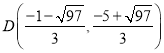
【解析】
(1)将A(4,0),B(2,0)代入y=ax2+bx+6(a≠0),求得![]() ;
;
(2)①由已知可求:![]() ,AE的直线解析式
,AE的直线解析式![]() ,设
,设![]() ,过点D与AE垂直的直线解析式为
,过点D与AE垂直的直线解析式为![]() ,两直线的交点为
,两直线的交点为![]() ,可求
,可求![]() ,则有当
,则有当![]() 时,DQ最大为
时,DQ最大为![]() ,则面积最大值为
,则面积最大值为![]() ;
;
②过点A作AN⊥DE,DE与x中交于点F,由tan∠AED=![]() ,可求AN=
,可求AN=![]() ,NE=3
,NE=3![]() ,因为Rt△AFN∽Rt△EFO,
,因为Rt△AFN∽Rt△EFO,![]() ,则有
,则有![]() ,所以F(2,0),得到EF直线解析式为y=x2,直线与抛物线的交点为D点.
,所以F(2,0),得到EF直线解析式为y=x2,直线与抛物线的交点为D点.
解:![]() 将
将![]() ,
,![]() 代入
代入![]() ,
,
可得![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() ,AE的直线解析式
,AE的直线解析式![]() ,
,
设![]() ,
,
过点D与AE垂直的直线解析式为![]() ,
,
两直线的交点为![]() ,
,
![]() ,
,
当![]() 时,DQ最大为
时,DQ最大为![]() ,
,
![]() ;
;
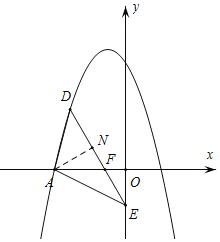
![]() 过点A作
过点A作![]() ,DE与x轴交于点F,
,DE与x轴交于点F,
![]() ,
,
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线解析式为
直线解析式为![]() ,
,
![]() 时,
时,![]() ,
,
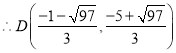 ;
;


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
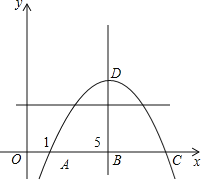
【题目】如图所示,抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5,且与x轴的左交点为(1,0),则下列说法正确的有( )
①C(9,0);②b+c>﹣10;③y的最大值为﹣16a;④若该抛物线与直线y=8有公共交点,则a的取值范围是a≤![]() .
.
A.①②③④B.①②③C.①③④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
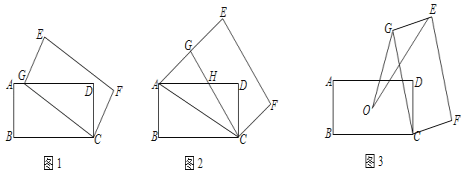
【题目】矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).
(1)如图1,当点G落在AD边上时,直接写出AG的长为 ;
(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;
(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD交于O点,DE∥AC,CE∥BD.
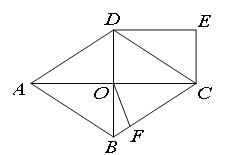
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,![]() ,顶点C的坐标为
,顶点C的坐标为![]() ,x反比例函数
,x反比例函数![]() 的图象与菱形对角线AO交于点D,连接BD,当
的图象与菱形对角线AO交于点D,连接BD,当![]() 轴时,k的值是______.
轴时,k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上.若BC=1,GH=2,则CG的长为( )
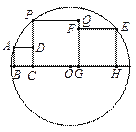
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),4x+2<kx+b<0的解集为( )
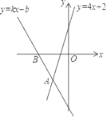
A.x<﹣2B.﹣2<x<﹣1C.x<﹣1D.x>﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
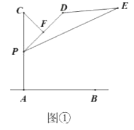
【题目】在炎热的夏季,遮阳伞在我们的生活中随处可见.如图①,滑动调节式遮阳伞的立柱![]() 直于地面
直于地面![]() ,点
,点![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
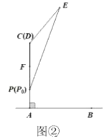
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
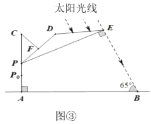
与![]() 重合(如图②).根据生活经验,当太阳光线与
重合(如图②).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为
垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为![]() (如图③),为使遮阳效果最佳,点
(如图③),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少米?(结果精确到
上调多少米?(结果精确到![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com