练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，点、、均在格点上.

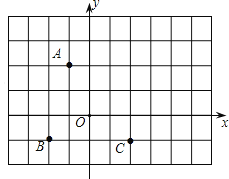
    （1）请直接写出点、、的坐标分别为_________，_________，_________.

    （2）若平移线段，使移动到的位置，请在图中画出移动后的位置，依次连接，，，，则四边形的面积为________.

    【答案】（1）A（1，2），B（2，1），C（2，1）；（2）12.

    【解析】

    （1）利用坐标系，根据各点所在象限的符号和距坐标轴的距离可得各点的坐标；

    （2）因为平移线段AB，使B移动到C的位置，所以A需相应的向右平移4格，即可作出图形，然后计算其面积即可．

    解：（1）A（1，2），B（2，1），C（2，1）；

    （2）画图如下：

    四边形ABCD的面积＝4×3＝12．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线与x轴交于点A、B（点A位于点B左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．

    （1）求点A、B、C的坐标；

    （2）设动点N（-2，n），求使MN+BN的值最小时n的值；

    （3）P是抛物线上位于x轴上方的一点，请探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

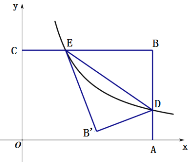
    【题目】如图，平面直角坐标系xOy中，线段BC∥x轴、线段AB∥y轴，点B坐标为(4，3)，反比例函数y＝（x＞0）的图像与线段AB交于点D，与线段BC交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，则点B'的纵坐标是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．

    （1）求抛物线的解析式和对称轴；

    （2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；

    （3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】悠悠食品店的A、B两种菜品，每份成本均为14元，售价分别为20元、18元，这两种菜品每天的营业额共为1120元，总利润为280元．

    （1）该店每天卖出这两种菜品共多少份？

    （2）该店为了增加利润，准备降低A种菜品的售价，同时提高B种菜品的售价，售卖时发现，A种菜品售价每降0.5元可多卖1份；B种菜品售价每提高0.5元就少卖1份，如果这两种菜品每天销售的总份数不变，这两种菜品一天的总利润是316元．求A种菜品每天销售多少份？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，阴影部分是边长为的大正方形中剪去一个边长为的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，下列四种割拼方法中，能够验证平方差公式的有（ ）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】菜矿泉水厂在山脚下筑有水池蓄水，山泉水不停地流入水池，水池底部有大小两个排水口，

    (1)当蓄水到吨时， 需要截住泉水清理水池。若开放小排水口小时，再开放大排水口分钟，能排完水池半的水:若同时开放两个排水口小时，刚好把水排完.求两个排水口每分钟的流量；

    (2)现关闭排水口，开放泉水放满水池后，泉水仍以固定的流量流入水池.若用-台抽水机抽水，小时刚好把水抽完；若用台抽水机抽水，分钟刚好把水抽完。证明:抽水机每分针的抽水量是泉水流量的倍；

    (3)在的条件下，若用台抽水机抽水，需要名长时间刚好把水池的水抽完？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（操作发现）如图1，为等腰直角三角形，，先将三角板的角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于），旋转后三角板的一直角边与交于点．在三角板另一直角边上取一点，使，线段上取点，使，连接，．

    （1）请求出的度数？

    （2）与相等吗？请说明理由；

    （类比探究）如图2，为等边三角形，先将三角板中的角与重合，再将三角板绕点按顺时针方向旋转（旋转角大于且小于）.旋转后三角板的一直角边与交于点.在三角板斜边上取一点，使，线段上取点，使，连接，.

    （3）直接写出_________度；

    （4）若，，求线段的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    同步练习册答案