
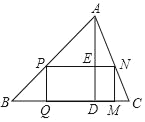
【题目】如图三角形ABC,BC=12,AD是BC边上的高AD=10.P,N分别是AB,AC边上的点,Q,M是BC上的点,连接PQMN,PN交AD于E.求
(1)若四边形PQMN是矩形,且PQ:PN=1:2.求PQ、PN的长;
(2)若四边形PQMN是矩形,求当矩形PQMN面积最大时,求最大面积和PQ、PN的长.

【答案】(1)PQ=![]() ,PN=
,PN=![]() ;(2)PQ=5,PN=6.
;(2)PQ=5,PN=6.
【解析】
(1)设PQ=y,则PN=2y,根据相似三角形的对应边上的高的比=相似比,构建方程即可解决问题;
(2)设AE=x.利用相似三角形的性质,用x表示PN,PQ,构建二次函数,利用二次函数的性质解决问题即可.
解:(1)设PQ=y,则PN=2y,
∵四边形PQMN是矩形,
∴PN∥BC,
∴△APN∽△ABC,
∵AD⊥BC,
∴AD⊥PN,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得y=![]() ,
,
∴PQ=![]() ,PN=
,PN=![]() .
.
(2)设AE=x.
∵四边形PQMN是矩形,
∴PN∥BC,
∴△APN∽△ABC,
∵AD⊥BC,
∴AD⊥PN,
∴![]() =
=![]() ,
,
∴PN=![]() x,PQ=DE=10﹣x,
x,PQ=DE=10﹣x,
∴S矩形PQMN=![]() x(10﹣x)=﹣
x(10﹣x)=﹣![]() (x﹣5)2+30,
(x﹣5)2+30,
∴当x=5时,S的最大值为30,
∴当AE=5时,矩形PQMN的面积最大,最大面积是30,
此时PQ=5,PN=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
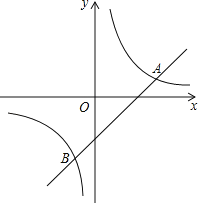
【题目】如图,在平面直角坐标系xOy中,直线y=x﹣2与双曲线y=![]() (k≠0)相交于A,B两点,且点A的横坐标是3.
(k≠0)相交于A,B两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线y=x﹣2交于点M,与双曲线y=![]() (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某农户利用一段墙体为一边(墙体的长为10米),用总长为40m的围网围成如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.

(1)求AE:EB的值;
(2)当BE的长为何值时,长方形ABCD的面积达到72m2?
(3)当BE的长为何值时,矩形区域①的面积达到最大值?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
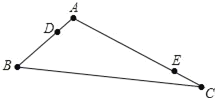
【题目】如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为2cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查本校学生对“关灯一小时”有关情况的了解程度.学校政教处随机抽取部分同学进行了调查,将调查结果分为:“A—不太了解、B—基本了解、C—了解较多、D—非常了解”四个等级,依据相关数据绘制成如下两幅统计图.

(1)这次调查抽取了多少名学生?
(2)根据两个统计图提供的信息,补全这两个统计图;
(3)若该校有 3000 名学生,请你估计全校对“关灯一小时”非常了解的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
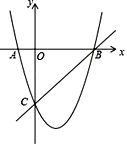
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)写出这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;不存在,请说明理由;
(3)过点P作x轴的垂线,交直线BC于点E,动点P运动到什么位置时,线段PE的值最大,求出此时P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
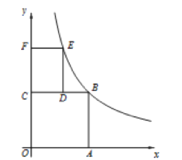
【题目】如图,正方形OABC的边OA,OC在坐标轴上,矩形CDEF的边CD在CB上,且5CD=3CB,边CF在轴上,且CF=2OC-3,反比例函数y=![]() (k>0)的图象经过点B,E,则点E的坐标是____
(k>0)的图象经过点B,E,则点E的坐标是____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com