
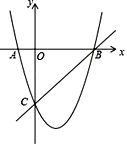
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ�����ͼ����������A(-1��0)��B(4��0)��C(0��-4)���㣬��P��ֱ��BC�·���������һ���㣮
��1��д��������κ����Ľ���ʽ��
��2���Ƿ���ڵ�P��ʹ��POC����OCΪ�ױߵĵ��������Σ������ڣ����P�����ꣻ�����ڣ���˵�����ɣ�
��3������P��x��Ĵ��ߣ���ֱ��BC�ڵ�E������P�˶���ʲôλ��ʱ���߶�PE��ֵ��������ʱP�����꣮
���𰸡���1��![]() ����2�����ڣ�(
����2�����ڣ�(![]() ����2)����3����m=2ʱ��PE��ֵ���ʱP������Ϊ(2��-6)
����2)����3����m=2ʱ��PE��ֵ���ʱP������Ϊ(2��-6)
��������
��1������֪�ĵ��������뺯������ʽ�����ô���ϵ����ֱ����⣮
��2�����á�POC����OCΪ�ױߵĵ��������Σ�����![]() ������P��OC�Ĵ�ֱƽ�����ϣ���P��ֱ��BC�·��������ϣ�����P�Ǵ�ֱƽ�����������ߵĽ��㣬ͨ���ⷽ�̵õ��𰸣�
������P��OC�Ĵ�ֱƽ�����ϣ���P��ֱ��BC�·��������ϣ�����P�Ǵ�ֱƽ�����������ߵĽ��㣬ͨ���ⷽ�̵õ��𰸣�
��3������P��x��Ĵ��ߣ���BC��E�����P�����꣬��֪E�ĺ�������P�ĺ�������ͬ������ֱ��BC�Ľ���ʽ��ʾE�������꣬��PE��![]() ����������ϵʽ�����ö��κ��������������ֵ���ɣ�
����������ϵʽ�����ö��κ��������������ֵ���ɣ�
�⣺��1����������Ϊ��![]()
��A(-1��0)��B(4��0)��C(0��-4)����ã�
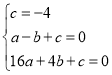 ��ã�
��ã�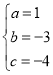
���������߽���ʽΪ![]()
��2����OC�Ĵ�ֱƽ����DP��
��OC�ڵ�D����BC�·�
�������ڵ�P����ͼ1��
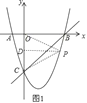
��PO=PD��
��ʱP�㼴Ϊ���������ĵ㣬
��C��0��-4����
��D��0����2����
��P����������2��
���������߽���ʽ�ɵ�![]() ��
��
���![]() ��С��0����ȥ����
��С��0����ȥ����
���������������P�㣬
��������![]() ����2��
����2��
��3���ߵ�P���������ϣ�
����P��m��m2-3m-4��
��B��4��0����C��0��-4��
����ֱ��B C�Ľ���ʽΪ��y=x-4
���E������m��m-4��
��PE= (m-4)-( m2-3m-4)
=-m2+4m
=-(m-2)2+4
��-1<0
�൱m=2ʱ��PE��ֵ���
��ʱP������Ϊ��2��-6��


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������Rt��ABC�У���A��90������D��E�ֱ��ڱ�AB��AC�ϣ�AD��AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮

��1���۲���룺ͼ1�У��߶�PM��PN��������ϵ���� ����λ�ù�ϵ���� ����
��2��̽��֤��������ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�����MN��BD��CE���ж���PMN����״����˵�����ɣ�
��3����չ���죺����ADE�Ƶ�A��ƽ����������ת����AD��8��AB��20����ֱ��д����PMN��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��BC��12��AD��BC���ϵĸ�AD��10��P��N�ֱ���AB��AC���ϵĵ㣬Q��M��BC�ϵĵ㣬����PQMN��PN��AD��E����
��1�����ı���PQMN�Ǿ��Σ���PQ��PN��1��2����PQ��PN�ij���
��2�����ı���PQMN�Ǿ��Σ�����PQMN������ʱ������������PQ��PN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
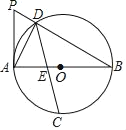
����Ŀ����ͼ��ABΪ��O��ֱ������AB��m��mΪ����������CΪ![]() ���е㣬��DΪԲ��һ���㣬��A������O�����߽�BD���ӳ����ڵ�P����CD��AB�ڵ�E��
���е㣬��DΪԲ��һ���㣬��A������O�����߽�BD���ӳ����ڵ�P����CD��AB�ڵ�E��
��1����DC��ABʱ����![]() ���� ����
���� ����
��2���ٵ���D��![]() ���ƶ�ʱ����̽���߶�DA��DB��DC֮���������ϵ����˵�����ɣ�
���ƶ�ʱ����̽���߶�DA��DB��DC֮���������ϵ����˵�����ɣ�
����CD��Ϊt�����ADB�����S��t�ĺ�����ϵʽ��
��3����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ��������ij�ҿ�ݹ�˾��2017��3�·���5�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
(1)��ÿ�ݹ�˾Ͷ�ݿ���ܼ�������ƽ����������
(2) ���ƽ��ÿ��ÿ������Ͷ�ݿ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ����2017��6�·ݵĿ��Ͷ������������ܣ�����������Ҫ���Ӽ���ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ij���۹��������ص�EΪ�ļ���Ŀ��������.��֪��E������������AB�ľ���OEΪ10��,����ABΪ123��(AB��ֱ����BC),�ڵ���C����õ�E�����Ǧ�=45��,�ӵ�C��CB����ǰ��40����D��,��D���������A�����Ǧ�=60��,���E�����ĸ߶�EF.(�����ȷ��0.1��)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ�
��abc��0����b��a+c����4a+2b+c��0����2c��3b����a+b��m��am+b����m��1��ʵ������
������ȷ�Ľ����У�������
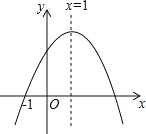
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
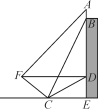
����Ŀ����ͼ��������ѧһ��ѧ¥��������һ���ΪAB�������ƣ���E�͵�D�ֱ��ǽ�ѧ¥�ײ�����ǽ�ϵ�һ��(A��B��D��E��ͬһֱ����)��С��ͬѧ�ھ�E��9��C����������Ƶײ���B������Ϊ67�㣬ͬʱ��ý�ѧ¥��ǽ���D������Ϊ30�㣬�ӵ�C���¶�Ϊ1��![]() ��б�������ߵ���Fʱ��DF������ˮƽ��CEƽ�У�
��б�������ߵ���Fʱ��DF������ˮƽ��CEƽ�У�
(1)���F��ֱ��CE�ľ���(�����������)��
(2)���ڵ�F����������ƶ���A������Ϊ45�㣬���������AB�ĸ߶�(�����ȷ��0.01)��(ע��sin67���0.92��tan67���2.36��![]() ��1.41��
��1.41��![]() ��1.73)
��1.73)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��һ����һ���������棬��������һ�µ��������ڹµ�P���ۿ�С����ְ��ں��л�������ͼ��ʾ����С����P���������ر�ƫ��60��������200��A�������������Ϸ�����һ��ʱ�䵽B������B��С���۲�������ڵ�P���ڱ�ƫ��37���ķ����ϣ���ʱС���������������ף���ȷ��1�ף���
���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com