
【题目】在![]() 中,
中,![]() ,CD是AB边上的高,若
,CD是AB边上的高,若![]() .
.

(1)求CD的长.
(2)动点P在边AB上从点A出发向点B运动,速度为1个单位/秒;动点Q在边AC上从点A出发向点C运动,速度为v个单位秒![]() ,设运动的时间为
,设运动的时间为![]() ,当点Q到点C时,两个点都停止运动.
,当点Q到点C时,两个点都停止运动.
①若当![]() 时,
时,![]() ,求t的值.
,求t的值.
②若在运动过程中存在某一时刻,使![]() 成立,求v关于t的函数表达式,并写出自变量t的取值范围.
成立,求v关于t的函数表达式,并写出自变量t的取值范围.
【答案】(1)CD=8;(2)t=4;(3)![]() (
(![]() )
)
【解析】
(1)作AE⊥BC于E,根据等腰三角形三线合一的性质可得BE=![]() BC,然后利用勾股定理求出AE,再用等面积法可求出CD的长;
BC,然后利用勾股定理求出AE,再用等面积法可求出CD的长;
(2)①过B作BF⊥AC于F,易得BF=CD,分别讨论Q点在AF和FC之间时,根据△BQF≌△CPD,得到PD=QF,建立方程即可求出t的值;
(3)同(2)建立等式关系即可得出关系式,再根据Q在FC之间求出t的取值范围即可.
解:(1)如图,作AE⊥BC于E,

∵AB=AC,
∴BE=![]() BC=
BC=![]()
在Rt△ABE中,
![]()
∵△ABC的面积=![]()
∴![]()
(2)过B作BQ⊥AC,当Q在AF之间时,如图所示,

∵△ABC的面积=![]() ,AB=AC
,AB=AC
∴BF=CD
在Rt△CPD和Rt△BQF中
∵CP=BQ,CD=BF,
∴Rt△CPD≌Rt△BQF(HL)
∴PD=QF
在Rt△ACD中,CD=8,AC=AB=10
∴![]()
同理可得AF=6
∴PD=AD=AP=6-t,QF=AF-AQ=6-2t
由PD=QF得6-t=6-2t,解得t=0,
∵t>0,
∴此种情况不符合题意,舍去;
当Q点在FC之间时,如图所示,

此时PD=6-t,QF=2t-6
由PD=QF得6-t=2t-6,
解得t=4,
综上得t的值为4.
(3)同(2)可知v>1时,Q在AF之间不存在CP=BQ,Q在FC之间存在CP=BQ,Q在F点时,显然CP≠BQ,
∵运动时间为t,则AP=t,AQ=vt,
∴PD=6-t,QF=vt-6,
由PD=QF得6-t=vt-6,
整理得![]() ,
,
∵Q在FC之间,即AF<AQ≤AC
∴![]() ,代入
,代入![]() 得
得
![]() ,解得
,解得![]()
所以答案为![]() (
(![]() )
)


科目:初中数学 来源: 题型:
【题目】若两个图形成中心对称,则下列说法:
①对应点的连线一定经过对称中心;
②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定互相平行;
④将一个图形围绕对称中心旋转![]() 后必与另一个图形重合.其中正确的有( )
后必与另一个图形重合.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶角为36°的等腰三角形,其底边与腰之比等![]() ,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
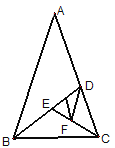
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=45°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在南偏西22°方向上.航行2小时后到达N处,观测灯塔P在南偏西44°方向上,若该船继续向南航行至离灯塔最近的位置,则此时轮船离灯塔的距离约为(参考数据:sin68°≈0.9272,sin46°≈0.7193,sin22°≈0.3746,sin44°≈0.6947)( )

A. 22.48海里 B. 41.68海里
C. 43.16海里 D. 55.63海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,CF⊥AC交AB的延长线于点F,G为BC的中点,射线AG交CF于D,E在CF上,CE=AD,连接BD,BE.求证:△BDE是等边三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点M在第二象限,且经过点 A(1,0)和点 B(0,2).则
(1)a 的取值范围是________;
(2)若△AMO的面积为△ABO面积的![]() 倍时,则a的值为________
倍时,则a的值为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com