
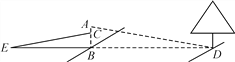
【题目】某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b (k≠0) 的图像与反比例函数y=-![]() 的图像交于A(-2,m)和B (n,-2) 两点,求:(1)一次函数的解析式;
的图像交于A(-2,m)和B (n,-2) 两点,求:(1)一次函数的解析式;
(2)△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,M为斜边AB上一点,且MB=MC=AC=8cm,平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移,运动到经过点M时停止. 直线l分别交线段MB、MC、AC于点D、E、P,以DE为边向下作等边△DEF,设△DEF与△MBC重叠部分的面积为S(cm2),直线l的运动时间为t(秒).

(1)求边BC的长度;
(2)求S与t的函数关系式;
(3)在整个运动过程中,是否存在这样的时刻t,使得以P、C、F为顶点的三角形为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
(4)在整个运动过程中,是否存在这样的时刻t,使得以点D为圆心、BD为半径的圆与直线EF相切?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
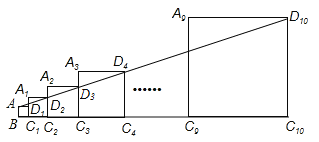
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
查看答案和解析>>
科目:初中数学 来源: 题型:
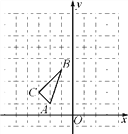
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;
(2)若点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
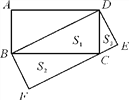
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1__ __S2+S3;(填“>”“=”或“<”)
(2)写出图中的三对相似三角形,并选择其中一对进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2![]() 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
(1)连接CQ,证明:CQ=AP;
(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE=![]() BC;
BC;
(3)猜想PF与EQ的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
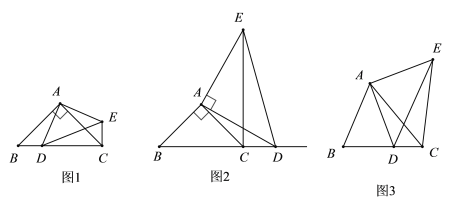
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com