
 在平面直角坐标系中,点A(-2a,a-1)在x轴上,将点A向右平移5个单位长度,向上平移m(m>2)个单位长度,得到点B,直线l是平行于x轴,纵坐标都是1的直线,点C与点B关于直线l轴对称.
在平面直角坐标系中,点A(-2a,a-1)在x轴上,将点A向右平移5个单位长度,向上平移m(m>2)个单位长度,得到点B,直线l是平行于x轴,纵坐标都是1的直线,点C与点B关于直线l轴对称.分析 (1)由点A在y轴上可求出a值,将其代入点A的坐标中即可得出点A的坐标,依据点的平移可得出点B的坐标,再根据点B、C关于直线l:y=1轴对称,即可求出点C的坐标;
(2)由点B、C的坐标可得出BC的长度,根据三角形的面积公式结合S△ABC=10,即可得出关于m的一元一次方程,解之即可得出m的值;
(3)设BC与x轴的交点为点D,则△AON∽△ADC,根据相似三角形的性质即可得出$\frac{AO}{AD}=\frac{ON}{DC}$,即$\frac{2}{5}=\frac{1}{m-2}$,解之经检验后即可得出m的值.
解答 解:(1)∵点A(-2a,a-1)在x轴上,
∴a-1=0,解得:a=1,
∴-2a=-2,
∴点A(-2,0).
∵将点A向右平移5个单位长度,向上平移m(m>2)个单位长度,得到点B,
∴点B(3,m).
∵点C与点B关于直线l:y=1轴对称,
∴点C(3,2-m).
(2)∵B(3,m),C(3,2-m),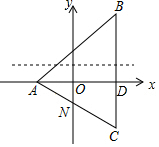
∴BC=2m-2,
∴S△ABC=$\frac{1}{2}$×5BC=5m-5=10,
解得:m=3.
(3)设BC与x轴的交点为点D,则△AON∽△ADC,如图所示.
∵△AON∽△ADC,
∴$\frac{AO}{AD}=\frac{ON}{DC}$,即$\frac{2}{5}=\frac{1}{m-2}$,
解得:m=$\frac{9}{2}$,
经检验,m=$\frac{9}{2}$是原分式方程的解.
点评 本题考查了两条直线相交或平行问题、坐标与图形变化中的平移及对称、解一元一次方程以及相似三角形的性质,解题的关键:(1)根据坐标的平移找出点B、C的坐标;(2)根据三角形的面积公式结合S△ABC=10列出关于m的一元一次方程;(3)根据相似三角形的性质列出$\frac{2}{5}=\frac{1}{m-2}$.


科目:初中数学 来源: 题型:选择题
| A. | 了解某路口每天在学校放学时段的车流量 | |
| B. | 检测某种新型LED灯的使用寿命 | |
| C. | 检测站对本市所有公交车的年度安全检查 | |
| D. | 了解同一批青菜的农药残留量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.
小明一家人春节期间参与了“支付宝集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给其中一个,两个人各设计了一个游戏,获胜者得到“敬业福”,请用适当的方法说明这两个游戏对小明和姐姐是否公平.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
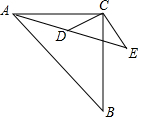 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
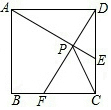 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=2,线段CP的最小值是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com