
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点, 求![]() 的值,并直接写出
的值,并直接写出![]() 的值.
的值.
【答案】(1)①4,②
【解析】
试题分析:(1)①令y=2代入y=x2,可求得A、B坐标,进而可求得AB长度,而AC=2AB,AC长度可求.②根据抛物线对称性可求得M坐标,利用顶点式设L2的解析式,再把B点坐标带入即可求得解析式;(2)过点B作BK⊥x轴于点K.设OK=t,则可利用t表示出G点坐标,L3解析式可表示出来,有因为L3经过点B代入化简就可求得![]() 的值,再利用L3解析式表示出顶点P的纵坐标,再代到L中可求得EF长度,
的值,再利用L3解析式表示出顶点P的纵坐标,再代到L中可求得EF长度,![]() 比值即可求出.
比值即可求出.
试题解析:(1)①对于二次函数y=x2,当y=2时,2=x2,解得x1=![]() ,x2=-
,x2=-![]() ,∴AB=2. ∵平移得到的抛物线L1经过点B,∴BC=AB=2,∴AC=4.② 记抛物线L2的对称轴与AD相交于点N,根据抛物线的轴对称性,得BN=DB=
,∴AB=2. ∵平移得到的抛物线L1经过点B,∴BC=AB=2,∴AC=4.② 记抛物线L2的对称轴与AD相交于点N,根据抛物线的轴对称性,得BN=DB=![]() , ∴
, ∴![]() .设抛物线L2的函数表达式为
.设抛物线L2的函数表达式为 .由①得,B点的坐标为(,2),∴
.由①得,B点的坐标为(,2),∴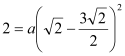 ,解得a=4.抛物线L2的函数表达式为
,解得a=4.抛物线L2的函数表达式为 .
.
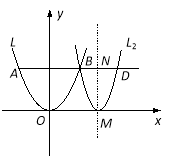
(2)如图,抛物线L3与x轴交于点G,其对称轴与x轴交于点Q,过点B作BK⊥x轴于点K.设OK=t,则AB=BD=2t, 点B的坐标为(t,at2),根据抛物线的轴对称性,得OQ=2t,OG=2OQ=4t.设抛物线L3的函数表达式为y=a3x(x-4t),∵该抛物线过点B(t,at2),∴at2=a3t(t-4t),因t≠0,得![]() .
.![]() .
.



科目:初中数学 来源: 题型:
【题目】点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,下列选项正确的是( )
A.PQ≥5
B.PQ>5
C.PQ<5
D.PQ≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上周五某股民小王买进某公司股票1000股,每股35元,下表为本周内每日股票的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +4 | +4.5 | ﹣1 | ﹣2.5 | ﹣4 |
则在星期五收盘时,每股的价格是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A. 200(1+a%)2=148 B. 200(1-a%)2=148
C. 200(1-2a%)=148 D. 200(1-a2%)=148
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一天中售出李宁牌运动鞋11双,其中各种尺码的鞋的销售量如下表所示,
鞋的尺码(单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
则这11双鞋的尺码组成一组数据中众数和中位数分别为( )
A. 25,25 B. 24.5,25 C. 26,25 D. 25,24.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com