
【题目】![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角
,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角![]() ,
,![]() .
.
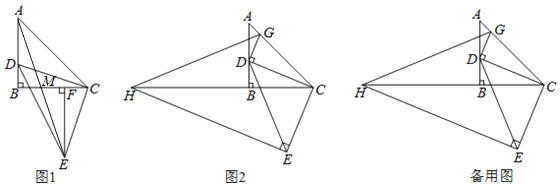
(1)如图1,作![]() 于F,求证:
于F,求证:![]() ;
;
(2)在图1中,连接AE交BC于M,求![]() 的值。
的值。
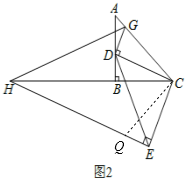
(3)如图2,过点E作![]() 交CB的延长线于点H,过点D作
交CB的延长线于点H,过点D作![]() ,交AC于点G,连接GH当点D在边AB上运动时,式子
,交AC于点G,连接GH当点D在边AB上运动时,式子![]() 的值会发生变化吗?若不变,求出该值:若变化请说明理由.
的值会发生变化吗?若不变,求出该值:若变化请说明理由.
【答案】(1)证明见解析;(2)2;(3)不变,理由见解析.
【解析】
(1)根据等腰直角三角形的性质得到CD=CE,再利用等角的余角相等得到∠DCB=∠CEF,然后根据“AAS”可证明△DBC≌△CFE;
(2)由△DBC≌△CFE得到BD=CF,BC=EF,再利用△ABC为等腰直角三角形得到AB=BC,所以AB=EF,AD=BF,接着证明△ABM≌△EFM,得到BM=FM,所以![]() ;
;
(3)在EH上截取EQ=DG,如图2,先证明△CDG≌△CEQ得到CG=CQ,∠DCG=∠ECQ,由于∠DCG+∠DCB=45°,则∠ECQ+∠DCB=45°,所以∠HCQ=45°,再证明△HCG≌△HCQ,则得到HG=HQ,然后可计算出![]() .
.
证明:(1)∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
又∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,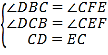 ,
,
∴△DBC≌△CFE;
(2)解:如图1,
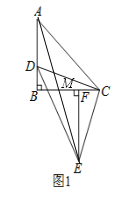
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,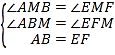 ,
,
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴![]()
(3)解:![]() 的值不变.
的值不变.
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中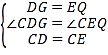 ,
,
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,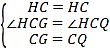 ,
,
∴△HCG≌△HCQ,
∴HG=HQ,
∴![]()
即式子![]() 的值不会发生变化.
的值不会发生变化.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
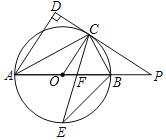
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
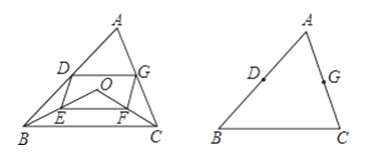
【题目】点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
(1)如图,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)当点O在△ABC外时,(1)的结论是否成立?(画出图形,指出结论,不需说明理由;)
(3)若四边形DEFG是菱形,则点O的位置应满足什么条件?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,线段AB、CD相交于点O,连接AD、CB,如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____________________;
(2)在图2中,若∠D=40°,∠B=30°,试求∠P的度数(写出解答过程);
(3)如果图2中,∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间的数量关系(直接写出结论即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
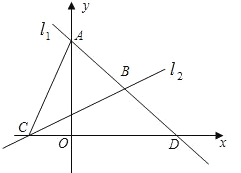
【题目】如图,直线l1过点A(0,4),点D(4,0),直线l2:![]() 与x轴交于点C,两直线
与x轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③c>0;④9a+3b+c<0。其中结论正确的有( )
的图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③c>0;④9a+3b+c<0。其中结论正确的有( )
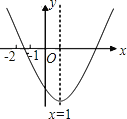
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)若M为AG中点,且DM=2,求DE的长;
(2)求证:AB=CF+DM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() ≠0
≠0![]() 的图像经过点(3,5)、(2,8)、(0,8).
的图像经过点(3,5)、(2,8)、(0,8).
①求这个二次函数的解析式;
②已知抛物线![]() ≠0
≠0![]() ,
,![]() ≠0
≠0![]() ,且满足
,且满足![]() ≠0,1
≠0,1![]() ,则我们称抛物线
,则我们称抛物线![]() 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当![]() 时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com