
【题目】如图,已知ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)若M为AG中点,且DM=2,求DE的长;
(2)求证:AB=CF+DM.

【答案】(1)DE=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由ABCD中,AE平分∠BAD交DC于E,DF⊥BC,易证得∠DMG=∠DGM,求得DG=DM=2,由直角三角形斜边上的中线等于斜边上的一半,求得AG的长,继而求得DE的长;
(2)此题有多种解法,通过构造不同的直角三角形,找到相应的全等三角形,在根据对应边和对应角相等,即可推出结论.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAE=∠DEA,
∵AE平分∠BAD,∴∠BAE=∠DAE
∴∠DAE=∠DEA,
∴DE=AD,
∵DF⊥BC,
∴DF⊥AD,
∵M为AG中点,
∴AG=2DM=4,
∵DN⊥CD,
∴∠ADM+∠MDG=∠MDG+∠EDG,
∴∠ADM=∠EDG,
∴∠DAE+∠ADM=∠DEA+∠EDG,
即∠DMG=∠DGM,
∴DG=DM=2,
在Rt△ADG中,DE=AD=![]() =
=![]() ;
;
(2)证法一:过点A作AD的垂线交DN的延长线于点H,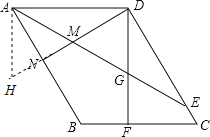
在△ADH和△FDC中,
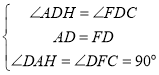 ,
,
∴△DAH≌△DFC(ASA),
∴AH=FC,DH=DC,
∵DF⊥AD,
∴AH∥DF,
∴∠HAM=∠DGM,
∵∠AMH=∠DMG,∠DMG=∠DGM,
∴∠HAM=∠HMA,
∴AH=MH,
∴MH=CF,
∴AB=CD=DH=MH+DM=CF+DM.
证法二:延长MD到点P,使DP=CF,连接PE
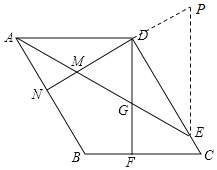
由(1)知AD=DE,
又AD=DF,
∴DF=DE,
∠DFC=∠EDP=90°
∴Rt△DCF≌Rt△EPD,
∴DC=EP,∠CDF=∠PED
∴PE∥DF,
∴∠PEA=∠DGA,
由(1)得∠DGA=∠DME,
∴∠PEA=∠DME
∴PM=PE,
而PM=DM+DP=DM+CF,PE=CD=AB,
∴AB=DM+FC.
证法三:过点A作AH⊥CB于点H,
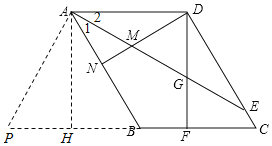
易证△ABH≌△DCF,
从而证得四边形AHFD为正方形.
把△ADG绕点A顺时针旋转90°,
得△AHP,∠AHP=∠AHB=90°
∴P、H、B三点共线
∵AE平分∠BAD,
∴∠1=∠2,而∠2=∠HAP,
∴∠HAB+∠1=∠HAB+∠HAP,即∠HAG=∠PAB
∵AH∥DF,
∴∠HAG=∠DGA
而∠DGA=∠APB
∴∠PAB=∠APB
∴AB=PB
∵PB=PH+HB=DG+FC
∴AB=DM+FC.
证法四:在DC上截取DP=DM,连接PF,

∵四边形ABCD是平行四边形,
∴AB∥CD
∴∠BAE=∠DEA,
而∠BAE=∠DAE,
∴∠DAE=∠DEADA=DE,
又∠ADF=∠MDE=90°,
∴∠ADM=∠EDG,
∴△ADM≌△EDG,
∴DM=DG,
∴DG=DP,
又AD=DF,
∴DF=DE,而∠PDF=∠FDP,
∴△PDF≌△GDE,
∴∠DPF=∠DGE,∠DFP=∠DEG,
∴∠CPF=∠DGM,
∵∠DFP+∠CFP=∠DEG+∠DMG=90°,
∴∠CFP=∠DMG,
而∠DMG=∠DGM,
∴∠CFP=∠CPFCF=CP,
而CD=DP+CP=DM+CF,AB=CD,
∴AB=DM+CF.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角
,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角![]() ,
,![]() .
.
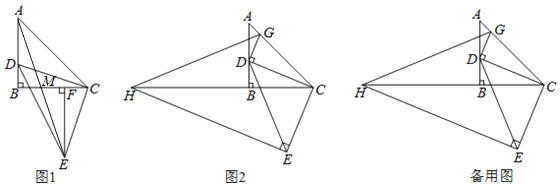
(1)如图1,作![]() 于F,求证:
于F,求证:![]() ;
;
(2)在图1中,连接AE交BC于M,求![]() 的值。
的值。
(3)如图2,过点E作![]() 交CB的延长线于点H,过点D作
交CB的延长线于点H,过点D作![]() ,交AC于点G,连接GH当点D在边AB上运动时,式子
,交AC于点G,连接GH当点D在边AB上运动时,式子![]() 的值会发生变化吗?若不变,求出该值:若变化请说明理由.
的值会发生变化吗?若不变,求出该值:若变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
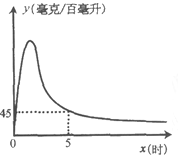
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.

(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 x 的一元二次方程 x![]() ﹣(m+2)x+3m﹣3=0.
﹣(m+2)x+3m﹣3=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于-2,求 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 y=-2x+4分别与 y 轴、x 轴交于点 A、点 B,点 C 的坐标为(-2,0),D 为线段 AB上一动点,连接 CD 交 y 轴于点 E.

(1)求出点 A、点 B 的坐标;
(2)若![]() ,求点 D 的坐标;
,求点 D 的坐标;
(3)在(2)的条件下,点 N 在 x 轴上,直线 AB 上是否存在点 M,使以 M,N,D,E 为顶点的四边形是平行四边形?若存在,请直接写出 M 点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
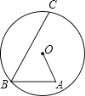
【题目】如图,在O内有折线OABC,点B、C在圆上,点A在O内,其中OA=4cm,BC=14cm,∠A=∠B=![]() ,则AB的长为__________________
,则AB的长为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com