
【题目】如图,直线 y=-2x+4分别与 y 轴、x 轴交于点 A、点 B,点 C 的坐标为(-2,0),D 为线段 AB上一动点,连接 CD 交 y 轴于点 E.

(1)求出点 A、点 B 的坐标;
(2)若![]() ,求点 D 的坐标;
,求点 D 的坐标;
(3)在(2)的条件下,点 N 在 x 轴上,直线 AB 上是否存在点 M,使以 M,N,D,E 为顶点的四边形是平行四边形?若存在,请直接写出 M 点的坐标;若不存在,请说明理由.
【答案】(1)A(0,4),B(2,0) ;(2)D(1,2);(3)存在,M( ![]() ,
, ![]() )或 M(
)或 M( ![]() ,-
,-![]() ).
).
【解析】
(1)先令![]() 求出y的值,再令y=0求出x的值即可得出A、B两点的坐标;
求出y的值,再令y=0求出x的值即可得出A、B两点的坐标;
(2)根据题意得![]() ,利用三角形面积公式可求得
,利用三角形面积公式可求得![]() =2,从而求得点D的坐标;
=2,从而求得点D的坐标;
(3)利用待定系数法求得直线CD的解析式,得到点E的坐标,分点N在线段OB上、点N在OB延长线上两种情况讨论,求得直线MN的解析式,利用求得两直线交点的方法即可求得点M的坐标.
(1)对于直线 y=-2x+4,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
∴A、B两点的坐标分别为(0,4)、(2,0);
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ×4×yD=
×4×yD=![]() ×4×2,
×4×2,
∴![]() =2,
=2,
∴点D的坐标为(1,2);
(3)设直线CD的解析式为![]() ,
,
把点C、D的坐标(-2,0)、(1,2)代入得:![]() ,
,
解得:![]() ,
,
∴直线CD的解析式为![]() ,
,
令![]() ,则
,则![]() ,
,
∴点E的坐标为(0,![]() );
);
①当点N在线段OB上时,DENM为平行四边形,如图:
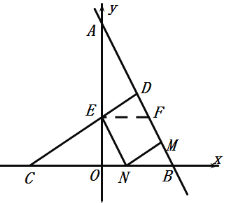
过E作EF∥OB交AB于点F,
∵点F在直线 y=-2x+4上,
∴点F的纵坐标与点E的纵坐标相等,
∴![]() =-2x+4,
=-2x+4,
∴点F的坐标为(![]() ,
,![]() ),
),
∵DENM为平行四边形,
∴EN∥DM,EN=DM,DE=MN,MN∥CD,
∵EF∥OB,
∴四边形EFBN也为平行四边形,
∴BN=EF=![]() ,
,
∴ON=2-![]() =
=![]() ,
,
∴点N的坐标为(![]() ,0),
,0),
设直线MN的解析式为![]() ,
,
将点N的坐标为(![]() ,0)代入得:
,0)代入得:![]() ,
,
∴直线MN的解析式为![]() ,
,
解方程组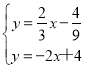 得:
得:![]() ,
,
∴点M的坐标为(![]() ,
,![]() );
);
②当点N在OB延长线上时,DENM为平行四边形,如图:
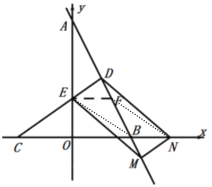
同理:BN=EF=![]() ,
,
∴ON=2+![]() =
=![]() ,
,
∴点N的坐标为(![]() ,0),
,0),
设直线MN的解析式为![]() ,
,
将点N的坐标为(![]() ,0)代入得:
,0)代入得:![]() ,
,
∴直线MN的解析式为![]() ,
,
解方程组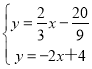 得:
得: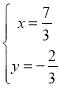 ,
,
∴点M的坐标为(![]() ,
,![]() );
);
综上,点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) .
) .


科目:初中数学 来源: 题型:
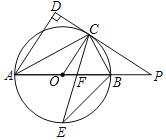
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
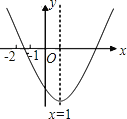
【题目】已知二次函数![]() 的图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③c>0;④9a+3b+c<0。其中结论正确的有( )
的图象如图所示,现有下列结论:①b2-4ac>0;②a>0;③c>0;④9a+3b+c<0。其中结论正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)若M为AG中点,且DM=2,求DE的长;
(2)求证:AB=CF+DM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小杰在学完了《锐角三角比》知识后回家整理笔记,写下了下列四句活:(1)锐角A的正弦的值的范围是0<sinA<1;(2)根据正切和余切的意义,可以得到tanA=![]() ;(3)在Rt△ABC中,如∠C=90°,则cosB=sinA;(4)在Rt△ABC中,如∠C=90°,则cotB=tanA;请你判断上述语句正确的个数是( )
;(3)在Rt△ABC中,如∠C=90°,则cosB=sinA;(4)在Rt△ABC中,如∠C=90°,则cotB=tanA;请你判断上述语句正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径作⊙O,过点A作⊙O的切线AC,连结BC,交⊙O于点D,点E是BC边的中点,连结AE.
(1)求证:∠AEB=2∠C;
(2)若AB=6,![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,二次函数![]() ≠0
≠0![]() 的图像经过点(3,5)、(2,8)、(0,8).
的图像经过点(3,5)、(2,8)、(0,8).
①求这个二次函数的解析式;
②已知抛物线![]() ≠0
≠0![]() ,
,![]() ≠0
≠0![]() ,且满足
,且满足![]() ≠0,1
≠0,1![]() ,则我们称抛物线
,则我们称抛物线![]() 互为“友好抛物线”,请写出当
互为“友好抛物线”,请写出当![]() 时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
时第①小题中的抛物线的友好抛物线,并求出这“友好抛物线”的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
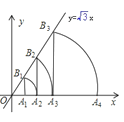
【题目】如图,直线![]() ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1B,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x的垂线交直线于点B2, 以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( )
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1B,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x的垂线交直线于点B2, 以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( )
A. (16,0) B. (12,0) C. (8,0) D. (32,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com