
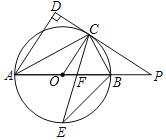
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
【答案】(1)证明见解析(2)证明见解析(3)4
【解析】
(1)根据切线的性质得OC⊥AD,而AD⊥DP,则肯定判断OC∥AD,根据平行线的性质得∠DAC=∠OCA,加上∠OAC=∠OCA,所以∠OAC=∠DAC;
(2)根据圆周角定理由AB为⊙O的直径得∠ACB=90°,则∠BCE=45°,再利用圆周角定理得∠BOE=2∠BCE=90°,则∠OFE+∠OEF=90°,易得∠CFP+∠OEF=90°,再根据切线的性质得到∠OCF+∠PCF=90°,而∠OCF=∠OEF,根据等角的余角相等得到∠PCF=∠CFP,于是可判断△PCF是等腰三角形;
(3)连结OE.由AB为⊙O的直径,得到∠ACB=90°,根据角平分线的定义得到∠BCE=45°,设⊙O的半径为r,则OF=6-r,根据勾股定理列方程即可得到结论.
(1)证明:∵PD为⊙O的切线,
∴OC⊥DP,
∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=∠DAC,
∴AC平分∠DAB;
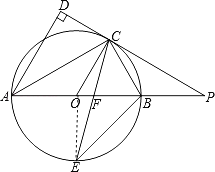
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠BCE=45°,
∴∠BOE=2∠BCE=90°,
∴∠OFE+∠OEF=90°,
而∠OFE=∠CFP,
∴∠CFP+∠OEF=90°,
∵OC⊥PD,
∴∠OCP=90°,即∠OCF+∠PCF=90°,
而∠OCF=∠OEF,
∴∠PCF=∠CFP,
∴△PCF是等腰三角形;
(3)解:连结OE.
∵AB为⊙O的直径,∴∠ACB=90°,
∵CE平分∠ACB,∴∠BCE=45°,
∴∠BOE=90°,即OE⊥AB,
设⊙O的半径为r,则OF=6-r,
在Rt△EOF中,∵OE2+OF2=EF2,
∴r2+(6-r)2=(2![]() )2,
)2,
解得,r1=4,r2=2,
当r1=4时,OF=6-r=2(符合题意),
当r2=2时,OF=6-r=4(不合题意,舍去),
∴⊙O的半径r=4.


科目:初中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,把
中,把![]() 、
、![]() 分别翻折,使点
分别翻折,使点![]() 、
、![]() 分别落在对角线
分别落在对角线![]() 上的点
上的点![]() 、
、![]() 处,折痕分别为
处,折痕分别为![]() 、
、![]() .
.
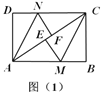
(1)求证:![]() .
.
(2)请连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 是平行四边形
是平行四边形
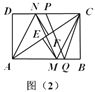
(3)![]() 、
、![]() 是矩形的边
是矩形的边![]() 、
、![]() 上的两点,连结
上的两点,连结![]() 、
、![]() 、
、![]() ,如图(2)所示,若
,如图(2)所示,若![]() ,
,![]() .且
.且![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
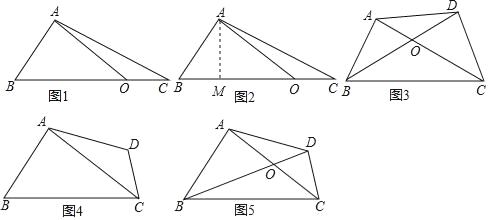
【题目】问题提出:某物业公司接收管理某小区后,准备进行绿化建设,现要将一块四边形的空地(如图5,四边形ABCD)铺上草皮,但由于年代久远,小区规划书上该空地的面积数据看不清了,仅仅留下两条对角线AC,BD的长度分别为20cm,30cm及夹角∠AOB为60°,你能利用这些数据,帮助物业人员求出这块空地的面积吗?
问题显然,要求四边形ABCD的面积,只要求出△ABD与△BCD(也可以是△ABC与△ACD)的面积,再相加就可以了.
建立模型:我们先来解决较简单的三角形的情况:
如图1,△ABC中,O为BC上任意一点(不与B,C两点重合),连接OA,OA=a,BC=b,∠AOB=α(α为OA与BC所夹较小的角),试用a,b,α表示△ABC的面积.
解:如图2,作AM⊥BC于点M,
∴△AOM为直角三角形.
又∵∠AOB=α,∴sinα=![]() 即AM=OAsinα
即AM=OAsinα
∴△ABC的面积=![]() BCAM=
BCAM=![]() BCOAsinα=
BCOAsinα=![]() absinα.
absinα.
问题解决:请你利用上面的方法,解决物业公司的问题.
如图3,四边形ABCD中,O为对角线AC,BD的交点,已知AC=20m,BD=30m,∠AOB=60°,求四边形ABCD的面积.(写出辅助线作法和必要的解答过程)
新建模型:若四边形ABCD中,O为对角线AC,BD的交点,已知AC=a,BD=b,∠AOB=α(α为OA与BC所夹较小的角),直接写出四边形ABCD的面积= .
模型应用:如图4,四边形ABCD中,AB+CD=BC,∠ABC=∠BCD=60°,已知AC=a,则四边形ABCD的面积为多少?(“新建模型”中的结论可直接利用)
查看答案和解析>>
科目:初中数学 来源: 题型:
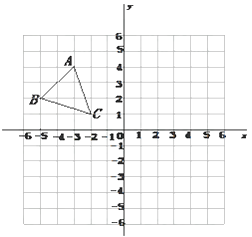
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中错误的有( )
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
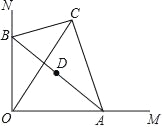
【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为![]() ;
;
其中正确的是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角
,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角![]() ,
,![]() .
.
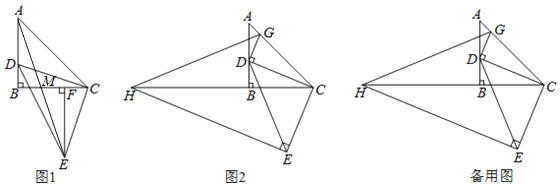
(1)如图1,作![]() 于F,求证:
于F,求证:![]() ;
;
(2)在图1中,连接AE交BC于M,求![]() 的值。
的值。
(3)如图2,过点E作![]() 交CB的延长线于点H,过点D作
交CB的延长线于点H,过点D作![]() ,交AC于点G,连接GH当点D在边AB上运动时,式子
,交AC于点G,连接GH当点D在边AB上运动时,式子![]() 的值会发生变化吗?若不变,求出该值:若变化请说明理由.
的值会发生变化吗?若不变,求出该值:若变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 y=-2x+4分别与 y 轴、x 轴交于点 A、点 B,点 C 的坐标为(-2,0),D 为线段 AB上一动点,连接 CD 交 y 轴于点 E.

(1)求出点 A、点 B 的坐标;
(2)若![]() ,求点 D 的坐标;
,求点 D 的坐标;
(3)在(2)的条件下,点 N 在 x 轴上,直线 AB 上是否存在点 M,使以 M,N,D,E 为顶点的四边形是平行四边形?若存在,请直接写出 M 点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com