
����Ŀ����֪:��ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB����ͼ2����ͼ1�������£���DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N���Խ���������⣺
(1)��ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ:_____________________��
(2)��ͼ2�У�����D=40������B=30���������P�Ķ���(д��������)��
(3)���ͼ2�У���D�͡�BΪ����ǣ������������䣬��д����P���D����B֮���������ϵ(ֱ��д�����ۼ���).

���𰸡���1����A+��D=��B+��C����2��35������3��2��P=��B+��D
��������
��1�����������ε��ڽǺ͵���180�����á�A+��D=��B+��C��
��2����ϸ�۲�ͼ2���õ�������ϵʽ��1+��D=��3+��P����2+��P=��4+��B�����ɽ�ƽ���ߵ����ʵá�1=��2����3=��4����ʽ��������ɵý��ۣ�
��3�����գ�2���Ľ���˼·.
�⣺��1����A+��D=��B+��C��
��2���ɣ�1���ã���1+��D=��3+��P����2+��P=��4+��B��
���1-��3=��P-��D����2-��4=��B-��P��
�֡�AP��CP�ֱ�ƽ�֡�DAB�͡�BCD��
���1=��2����3=��4��
���P-��D=��B-��P��
��2��P=��B+��D��
���P=��40��+30������2=35����
��3���ɣ�2���Ľ��ⲽ���֪����P���D����B֮���������ϵΪ��2��P=��B+��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
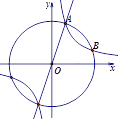
����Ŀ����ͼ����֪����![]() ��
��![]() ��ͼ���ڵ�һ�����ڵ�A��m,y1��,��B��m+1��y2����
��ͼ���ڵ�һ�����ڵ�A��m,y1��,��B��m+1��y2����![]() ��ͼ���ϣ��ҵ�B����O ��ΪԲ�ģ�OAΪ�뾶�ġ�O��,��k��ֵΪ�� ��.
��ͼ���ϣ��ҵ�B����O ��ΪԲ�ģ�OAΪ�뾶�ġ�O��,��k��ֵΪ�� ��.
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
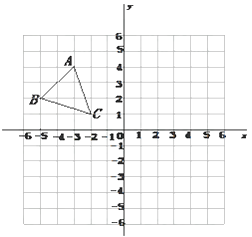
����Ŀ����ͼ��ƽ��ֱ������ϵ�ڣ�С����������ı߳�Ϊ1����λ���ȣ���ABC ���������������ֱ� A��-3��4��B��-5��2��C��-2��1��
��1������ ��ABC����y ��ĶԳ�ͼ�� ��A1B1C1��
��2����������ABC ��ԭ�� O��ʱ�뷽����ת90���õ�����A2B2C2 ��
��3����2�����߶� OAɨ����ͼ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
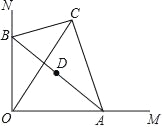
����Ŀ����ͼ����Rt��ABC�У�BC=2����BAC=30�㣬б��AB�������˵�ֱ������ֱ������OM��ON�ϻ��������н��ۣ�
����C��O�������AB�Գƣ���OA=2![]() ��
��
��C��O�����������ֵΪ4��
����ABƽ��CO����AB��CO��
��б��AB���е�D�˶�·���ij�Ϊ![]() ��
��
������ȷ����_____��������Ϊ��ȷ���۵���Ŷ����ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10������Rt��ABC�У���BAC=![]() ,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��
,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��

��1����֤����AEF����DEB��
��2��֤���ı���ADCF�����Σ�
��3����AC=4��AB=5��������ADCFD �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�![]() ����D��AB���ϣ������A��B�غϣ�����CDΪ��������ֱ��
����D��AB���ϣ������A��B�غϣ�����CDΪ��������ֱ��![]() ��
��![]() .
.
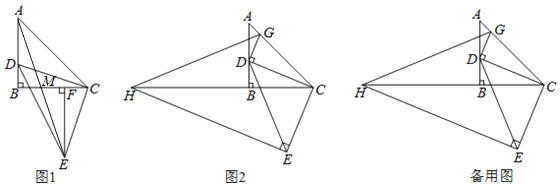
��1����ͼ1����![]() ��F����֤��
��F����֤��![]() ��
��
��2����ͼ1�У�����AE��BC��M����![]() ��ֵ��
��ֵ��
��3����ͼ2������E��![]() ��CB���ӳ����ڵ�H������D��
��CB���ӳ����ڵ�H������D��![]() ����AC�ڵ�G������GH����D�ڱ�AB���˶�ʱ��ʽ��
����AC�ڵ�G������GH����D�ڱ�AB���˶�ʱ��ʽ��![]() ��ֵ�ᷢ���仯�������䣬�����ֵ�����仯��˵������.
��ֵ�ᷢ���仯�������䣬�����ֵ�����仯��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʯ����ϩ��ij���������ס����������ϵ������Ϣ���±����������������⣺
������ | �ɱ��� | ���۴����� | |
�������� | 2100��Ԫ/�֣� | 800��Ԫ/�֣� | 200��Ԫ/�֣� |
�������� | 2400��Ԫ/�֣� | 1100��Ԫ/�֣� | 100��Ԫ/�֣� ��ÿ�»���֧���豸������ά����20000Ԫ |
��1����ó���ÿ�������ס����������ϸ�x�֣�����ֱ�Ϊy1Ԫ��y2Ԫ���ֱ����y1��y2��x�ĺ�����ϵʽ(ע������=������-��֧��)��
��2����֪�ó���ÿ�������ס����������Ͼ�������400�֣���ij��Ҫ�����ס����������Ϲ�700�֣�����������ס������ϸ����ٶ�ʱ����õ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�ı߳���2��D��E�ֱ�ΪAB��AC���е㣬�ӳ�BC����F��ʹCF=![]() BC������CD��EF��
BC������CD��EF��

��1����֤��DE=CF��
��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C����������y=ax2��2amx+am2+2m��5�����Щ�![]() ��a��0���ϣ�AB��x�ᣬ��ABC=135������AB=4��
��a��0���ϣ�AB��x�ᣬ��ABC=135������AB=4��
��1����գ������ߵĶ�������Ϊ ���ú�m�Ĵ���ʽ��ʾ����
��2������ABC��������ú�a�Ĵ���ʽ��ʾ����
��3������ABC�����Ϊ2����2m��5��x��2m��2ʱ��y�����ֵΪ2����m��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com