
【题目】解不等式2x﹣3< ![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. ![]()
【答案】解:先去分母,得3(2x﹣3)<x+1 去括号,得6x﹣9<x+1
移项,得5x<10
系数化为1,得x<2
∴原不等式的解集为:x<2,
在数轴上表示为:![]()
【解析】先去分母,再去括号、移项、合并同类项,系数化为1,求出不等式的解集,再在数轴上表示出来即可.
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈,以及对一元一次不等式的解法的理解,了解步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: 
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( ) 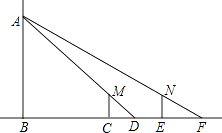
A.4.5米
B.6米
C.7.2米
D.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2. 
(1)求证:∠ABC=∠D;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的 ![]() ,设人行通道的宽度为x千米,则下列方程正确的是( )
,设人行通道的宽度为x千米,则下列方程正确的是( )
A.(2﹣3x)(1﹣2x)=1
B.![]()
(2﹣3x)(1﹣2x)=1
C.![]()
(2﹣3x)(1﹣2x)=1
D.![]()
(2﹣3x)(1﹣2x)=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com