
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若∠BOC=130°,∠ABC:∠ACB=3:2,求∠AEF和∠EFC.
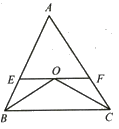
【答案】∠AEF=60°,∠EFC=140°.
【解析】
先根据三角形内角和定理,求出∠OBC+∠OCB的度数,再根据角平分线定义和已知中的∠ABC:∠ACB=3:2,求出∠ABC、∠ACB的度数,最后依据平行线的性质求出∠AEF和∠EFC的度数.
∵∠ABC: ∠ACB=3:2,
∴设∠ABC=3x, ∠ACB=2x,
∵BO、CO分别平分 ∠ ABC、 ∠ ACB,
∴∠ABO=∠CBO=![]() x,∠ACO=∠BCO=x,
x,∠ACO=∠BCO=x,
又∵∠BOC=130°,
在△BOC中,∠BOC+∠OBC+∠OCB=180°,
∴130°+![]() x+x=180°,
x+x=180°,
解得:x=20°,
∴∠ABC=3x=60°, ∠ACB=2x=40°,
∵EF∥BC,
∴∠AEF=∠ABC=60°,
∠EFC+∠ACB=180°,
∴∠EFC=140°.


科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( ) 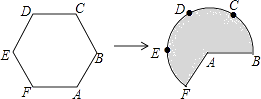
A.6π
B.18
C.18π
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
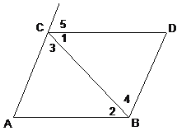
【题目】如图,完成下列推理过程,已知AB∥CD,AC∥BD,
(1)∵AB∥CD(已知) ∴∠A=∠5(两直线平行,_______________);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,_______________);
(3)∵AB∥CD(已知) ∴∠__=∠___(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D +∠______ =180°(两直线平行,____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1000元购进一批套尺,很快销售一空;商店又用1500元购进第二批同款套尺,购进单价比第一批贵25%,所购数量比第一批多100套.
(1)求第一批套尺购进的单价;
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境、低碳出行已渐渐成为人们的习惯.最近无为县城又引进了共享单车,只需要交点押金,就可以通过扫描二维码的方式解锁一辆停在路边的自行车,以极低的费用,轻松骑到目的地.王老师家与学校相距2km,现在每天骑共享单车到学校所花的时间比过去骑电动车多用4min.已知王老师骑电动车的速度是骑共享单车速度的1.5倍,则王老师骑共享单车的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 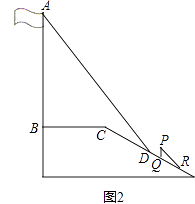
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( ) 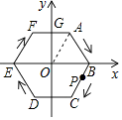
A.(1, ![]() )
)
B.(﹣1,﹣ ![]() )
)
C.(1,﹣ ![]() )
)
D.(﹣1, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com