
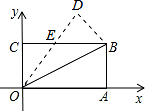
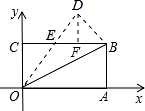
如图,在矩形 OABC 中,OA=8,OC=4,沿对角线 OB 折叠后,点 A 与点 D 重合,OD 与 BC
交于点 E,则点 D 的坐标是( )
A.(4,8) B.(5,8) C.(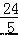 ,
,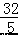 ) D.(
) D.(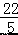 ,
,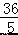 )
)
C【考点】翻折变换(折叠问题);坐标与图形性质.
【专题】计算题;压轴题.
【分析】由四边形 ABCD 为矩形,利用矩形的性质得到两对边相等,再利用折叠的性质得到 OA=OD, 两对角相等,利用 HL 得到直角三角形 BOC 与直角三角形 BOD 全等,利用全等三角形对应角相等 及等角对等边得到 OE=EB,在直角三角形 OCE 中,设 CE=x,表示出 OE,利用勾股定理求出 x 的 值,确定出 CE 与 OE 的长,进而由三角形 COE 与三角形 DEF 相似,求出 DF 与 EF 的长,即可确 定出 D 坐标.
【解答】解:∵矩形 ABCO 中,OA=8,OC=4,
∴BC=OA=8,AB=OC=4,
由折叠得到 OD=OA=BC,∠AOB=∠DOB,∠ODB=∠BAO=90°, 在 Rt△CBO 和 Rt△DOB 中,
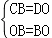 ,
,
∴Rt△CBO≌Rt△DOB(HL),
∴∠CBO=∠DOB,
∴OE=EB,
设 CE=x,则 EB=OE=8﹣x,
在 Rt△COE 中,根据勾股定理得:(8﹣x)2=x2+42, 解得:x=3,
∴CE=3,OE=5,DE=3,
过 D 作 DF⊥BC,可得△COE∽△FDE,
∴ 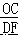 =
= 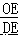 =
= 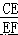 ,即
,即 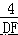 =
= 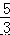 =
= 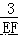 , 解得:DF=
, 解得:DF= 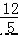 ,EF=
,EF= 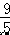 ,
,
∴DF+OC= 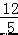 +4=
+4= 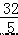 ,CF=3+
,CF=3+ 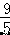 =
= 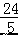 ,
,
则 D(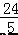 ,
,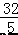 ), 故选 C.
), 故选 C.
【点评】此题考查了翻折变换(折叠问题),坐标与图形性质,全等三角形的判定与性质,勾股定理, 熟练掌握折叠的性质是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
按要求分别写出一个大于9且小于10的无理数:
(1)用一个平方根表示: ;
(2)用一个立方根表示: ;
(3)用含π的式子表示: ;
(4)用构造的方法表示: .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABO的顶点A是双曲线y1=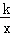 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=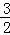 .
.
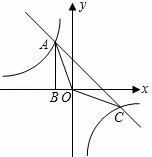 (1)求这两个函数的解析式;
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,把点 P(﹣3,2)绕原点 O 顺时针旋转 180°,所得到的对应点 P′的坐标为
( )
A.(3,2) B. C.(﹣3,﹣2) D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
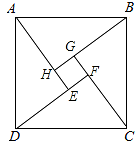
如图是“赵爽弦图”,△ABH、△BCG、△CDF 和△DAE 是四个全等的直角三角形,四边形 ABCD
和 EFGH 都是正方形.如果 AB=10,EF=2,那么 AH 等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场统计了今年 1~5 月 A,B 两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图

(1)分别求该商场这段时间内 A,B 两种品牌冰箱月销售量的中位数和方差; 根据计算结果,比较该商场 1~5 月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com