
【题目】如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
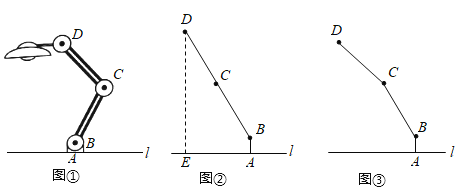
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
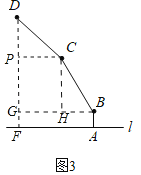
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
【答案】(1)连杆端点D离桌面l的高度DE为37cm;(2)4.
【解析】
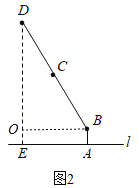
(1)如图2中,作BO⊥DE于O.解直角三角形求出OD即可解决问题.
(2)作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,求出DF,再求出DF﹣DE即可解决问题.
解:(1)作BF⊥DE于点F,则∠BFE=∠BFD=90°,
∵DE⊥l,AB⊥l,
∴∠BEA=∠BAE=90°=∠BFE.
∴四边形ABFE为矩形.
∴EF=AB=5cm,EF∥AB,
∵EF∥AB,
∴∠D+∠ABD=180°,
∵∠ABD=143°,
∴∠D=37°,
在Rt△BDF中,∵∠BFD=90°,
∴![]() =cosD=cos37°=0.8,
=cosD=cos37°=0.8,
∵DB=DC+BC=20+20=40,
∴DF=40×0.8=32,
∴DE=DF+EF=32+5=37cm,
答:连杆端点D离桌面l的高度DE为37cm;
(2)如图3,作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,
∵∠CBH=53°,∠CHB=90°,
∴∠BCH=37°,
∵∠BCD=180°﹣16°=164°,∠DCP=37°,
∴CH=BCsin53°=20×0.8=16(cm),DP=CDsin37°=20×0.6=12(cm),
∴DF=DP+PG+GF=DP+CH+AB=12+16+5=33(cm),
∴下降高度:DE﹣DF=37﹣33=4(cm).
故答案为:4.


科目:初中数学 来源: 题型:
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
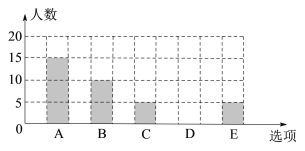
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.
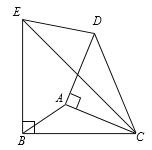
(1)求证:△DAC∽△EBC;
(2)求△ABC与△DEC的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,点C在半圆O上,AB=8,∠CAB=60°,P是弧![]() 上的一个点,连接AP,过点C作CD⊥AP于点D,连接BD,在点P移动过程中,BD长的最小值为_____.
上的一个点,连接AP,过点C作CD⊥AP于点D,连接BD,在点P移动过程中,BD长的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(4,0)和(0,3),动点P从点A出发,以每秒2个长度单位的速度沿AO向O运动,在点P出发的同时,动直线EF从x轴出发,以每秒1个长度单位沿y轴方向向上平移,分别与y轴、线段AB交于EP、FP.设运动时间为ts(0<t≤2).
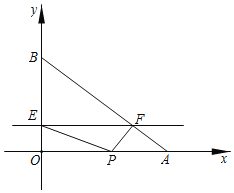
(1)在运动过程中,是否存在某一时刻t,使得△EOP与△AOB相似?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
(2)若△PEF是等腰三角形,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;
![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;
![]() ;
;
![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(2,0),对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:其中正确的是( )
①抛物线过原点:
②a﹣b+c<0:
③2a+b+c=0;
④抛物线顶点为(1,![]() ):
):
⑤当x<1时,y随x的增大而增大
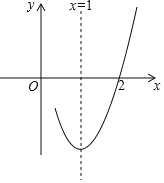
A.①②③B.①③④C.①④⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
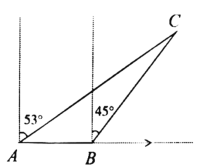
【题目】如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行![]() 后达到B处(
后达到B处(![]() ),测得小岛C位于它的北偏东45°方向.小岛C的周围
),测得小岛C位于它的北偏东45°方向.小岛C的周围![]() 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1,h2,h3,△ABC的高为h.
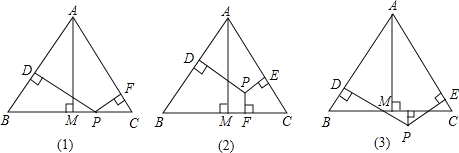
(1)若点P在一边BC上,如图①,此时h3=0,求证:h1+h2+h3=h;
(2)当点P在△ABC内,如图②,以及点P在△ABC外,如图③,这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1,h2,h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com